58X=40X:47=2325X=49×38X+79X=43.-数学
| 4 |
| 3 |
| 16 |
| 9 |
| 4 |
| 3 |
| 16 |
| 9 |
| 9 |
| 16 |
| 4 |
| 3 |
| 9 |
| 16 |
X=
| 3 |
| 4 |
据专家权威分析,试题“58X=40X:47=2325X=49×38X+79X=43.-数学-”主要考查你对 解方程,函数的奇偶性、周期性 等考点的理解。关于这些考点的“档案”如下:
解方程函数的奇偶性、周期性
考点名称:解方程
- 解方程:
使方程左右两边相等的未知数的值叫做方程的解。
求方程的解的过程叫做解方程。
方程的解是一个值,解方程是求方程的解的演算过程。
检验方法:
求出未知数的值分别代入原方程的两边计算(即含有字母的式子的值),如果原方程等号左右两边相等,则所求得的未知数的值是原方程的解。 - 解方程依据:
方程依靠等式各部分的关系,和加减乘除各部分的关系:
加数+加数=和,和-其中一个加数=另一个加数,差+减数=被减数,
被减数-减数=差,被减数-差=减数,
因数×因数=积,积÷一个因数=另一个因数,
被除数÷除数=商,被除数÷商=除数,商×除数=被除数。
考点名称:函数的奇偶性、周期性
函数的奇偶性定义:
偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),则称函数f(x)为偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)是奇函数。
函数的周期性:(1)定义:若T为非零常数,对于定义域内的任一x,使f(x+T)=f(x)恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
周期函数定义域必是无界的。
(2)若T是周期,则k·T(k≠0,k∈Z)也是周期,所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期,如常函数f(x)=C。奇函数与偶函数性质:
(1)奇函数与偶函数的图像的对称性:奇函数的图像关于原点对称,偶函数的图像关于y轴对称。
(3)在公共定义域内,①两个奇函数的和是奇函数,两个奇函数的积是偶函数; ②两个偶函数的和、积是偶函数; ③一个奇函数,一个偶函数的积是奇函数。注:定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
1、函数是奇函数或偶函数的前提定义域必须关于原点对称;定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
2、函数的周期性 令a , b 均不为零,若:
(1)函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a|
(2)函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a|
(3)函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a|
(4)函数y = f(x) 存在 f(x + a) =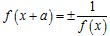 ==> 函数最小正周期 T=|2a|
==> 函数最小正周期 T=|2a|
(5)函数y = f(x) 存在 f(x + a) = ==> 函数最小正周期 T=|4a|
==> 函数最小正周期 T=|4a|
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |