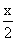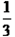题文

只列式（或方程）不计算． （1）明明家这个月交了240元水电费，比上个月节约了60元，节约了百分之几？______． （2）飞机的速度是每小时860千米，比火车速度的8倍少20千米．求火车的速度．______． （3）明明过生日时请好朋友们吃饭，买了4瓶橙汁，每瓶0.75升，每杯可倒 3 10 升，这些橙汁可倒多少杯？______． （4）蜗牛5分钟爬行了41厘米，照这样的速度，蜗牛爬行了61.5厘米要多少分钟？______．

题型：解答题  难度：中档

答案

（1）60÷（60+240）； （2）设火车的速度为每小时x千米，     8x-20=860； （3）4×0.75÷ 3 10 ； （4）设蜗牛爬行了61.5厘米要x分钟，     41 5 = 61.5 x ．

据专家权威分析，试题“只列式（或方程）不计算．（1）明明家这个月交了240元水电费，比上个月..”主要考查你对  列方程解决问题，百分数的计算，百分数的应用题，解比例，比例的应用题，整数，小数，分数，百分数和比例的复合应用题  等考点的理解。关于这些考点的“档案”如下：

列方程解决问题百分数的计算，百分数的应用题解比例，比例的应用题整数，小数，分数，百分数和比例的复合应用题

考点名称：列方程解决问题

• 列方程解决问题：
  未知数用字母表示，参加列式。根据题意找出数量间的相等关系，列出含有未知数的等式，也就是方程。
  它的优势体现在可以使未知数直接参加运算。

• 列方程解决问题一般步骤：
  ①审题，弄清题意：即全面分析已知数与已知数、已知数与未知数的关系。特别要把牵涉到的一些概念术语弄清，如同向，相向，增加到，增加了等。
  ②引进未知数：用x表示所求的数量或有关的未知量。在小学阶段所遇到的应用题并不十分复杂，一般只需要直接把要求的数量设为未知数。
  ③找出应用题中数量间的相等关系，列出方程。
  ④解方程，找出未知数的值。
  ⑤检验并写出答案：检验时，
  一是要将所求得的未知数的值代太原方程，检验方程的解是否正确；
  二是检查所求得的未知数的值是否符合题意，不符合题意的要舍去，保留符合题意的解。

考点名称：百分数的计算，百分数的应用题

• 常见的百分数的计算方法：
  

• 百分数应用题关系式：
  利息的计算公式：利息=本金×利率×时间。 
  百分率：例：发芽率=发芽种子数÷试验种子数×100%
  利率=利息÷本金×100%
  折数=现价÷原价
  成数=实际收成÷计划收成
  税率=应纳税额÷总收入×100%
  利润=售出价-成本，利润率=利润÷成本×100%=（售出价÷成本-1）×100%
  折扣=实际售价÷原售价×100%（折扣<1）
  浓度问题：
  溶质的重量+溶剂的重量=溶液的重量； 
  溶质的重量÷溶液的重量×100%=浓度； 
  溶液的重量×浓度=溶质的重量； 
  溶质的重量÷浓度=溶液的重量。

考点名称：解比例，比例的应用题

• 解比例：
  求比例中的未知项，叫做解比例。
  根据比例的基本性质（即交叉相乘），如果已知比例中的任何三项，就可以求出这个比例中的另外一个未知项。求比例中的未知项，叫做解比例。解比例是利用比例的基本性质：在比例中，两个外项的积等于两个内项的积。再转化成方程。
  
  比例应用题：
  是小学六年级奥数中的一个重要内容。它既是整数应用题的继续与深化，又是学习更多数学知识的重要基础，同时，这类题又有着自身的特点和解题的规律。在处理几个量的倍比关系时，比例应用题与分数百分数应用题间有很多相似之处，但利用比例处理问题要方便灵活得多。 
  要解决好此类问题，须注意灵活运用画线段示意图等手段，多角度、多侧面思考问题。在解题过程中，要善于掌握对应、假设、转化等多种解题方法，在寻找正确的解题方法的同时，不断地开拓解题思路。

• 用比例方法解应用题的一般步骤：
  

考点名称：整数，小数，分数，百分数和比例的复合应用题

• 含有小数、分数、百分数、比例中任意两种或两种以上的数的运算应用题。
  复合应用题：
  是由两个或两个以上相互联系的简单应用题组合而成的。
  在这种应用题中有两个或两个以上相互关联的数量关系，而且所求问题需要的条件没有直接给出。
  这就要根据相互关联的数量关系找出已知数量和未知数量的联系，先解答一个或几个中间问题，也就是把它先分解成几个简单应用题，然后再根据它们的联系依次列式并求解。