一个直角三角形的两个锐角的度数成反比例。[]-六年级数学
题文
| 一个直角三角形的两个锐角的度数成反比例。 |
|
[ ] |
答案
| 错误 |
据专家权威分析,试题“一个直角三角形的两个锐角的度数成反比例。[]-六年级数学-”主要考查你对 三角形的分类,正比例的意义,反比例的意义 等考点的理解。关于这些考点的“档案”如下:
三角形的分类正比例的意义,反比例的意义
考点名称:三角形的分类
学习目标:
探究掌握三角形的分类标准及方法,体会每类三角形特征,并能够识别直角三角形、锐角三角形、钝角三角形,等腰三角形和等边三角形。按角分:
1、锐角三角形:三个角都是锐角
2、直角三角形:有一个角是直角,两个锐角
3、钝角三角形:有一个钝角,两个锐角
特别提醒:每个三角形都至少有两个锐角。按边分:
1、等腰三角形:2条边相等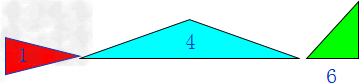
2、等边三角形:3条边都相等
3、不等边三角形:3条边都不相等
考点名称:正比例的意义,反比例的意义
正比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线;
用字母表示为如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示: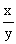 =k(一定);
=k(一定);
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变.正比例和反比例
反比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;
如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定)。- 反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
成反比例的量:
前提:两种相关的量(乘法关系)
要求:一个量变化,另一个量也随着变化,并且,这两个量中相对应的两个数的乘积一定。
结论:这两个量就叫做反比例的量,它们的关系叫做反比例关系。 正比例和反比例关系:
相同点:
①正比例和反比例都含有三个数量,在这三个数量中,均有一个定量、两个变量。
②在正、反比例的两个变量中,均是一个量变化,另一个量也随之变化。并且变化方式均属于扩大(乘以一个数)或缩小(除以一个数)若干倍的变化。
不同点:
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线;反比例是曲线。
③公式不同:正比例是(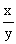 =k(一定)),反比例是(xy=k(一定))。
=k(一定)),反比例是(xy=k(一定))。
④规律不同:正比例是一个数缩小,另一个数也缩小,一个数扩大,另一个数也扩大;反比例是一个数缩小,另一个数就扩大,一个数扩大另一个数就缩小。- 判断两种量成正比例、反比例或不成比例的方法:
(1)找出两种相关联的量。
(2)根据两种相关联的量之间的关系列出数量关系式。
(3)如果两种量中相对应的两个数的比值(也就是商)一定,就是成正比例的量;若积一定,就是反比例的量。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![三角形中最大的一个角是61°,按角分类这是一个锐角三角形。[]-六年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/sanjiaoxingdefenlei/2019-04-05/8cc8f71e7f4757b1804275ceef5dce6f.gif)



