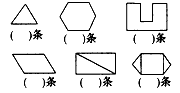
判断题。(对的在括号里打“√”,错误的打“×”)(1)角的两边越长,角就越大。[](2)长方形、正方形和圆都是轴对称图形。[](3)1的倒数是1,0的倒数是0。[](4)正方形的边长与面积成正-六年级数学
题文
判断题。(对的在括号里打“√”,错误的打 “×”)
|
答案
| (1)×;(2)√;(3)×;(4)× |
据专家权威分析,试题“判断题。(对的在括号里打“√”,错误的打“×”)(1)角的两边越长,角就..”主要考查你对 直线,射线,线段,角,度,轴对称,轴对称图形,倒数,正比例的意义,反比例的意义 等考点的理解。关于这些考点的“档案”如下:
直线,射线,线段,角,度轴对称,轴对称图形倒数正比例的意义,反比例的意义
考点名称:直线,射线,线段,角,度
直线:
把线段的两端无限延长,可以得到一条直线;
直线l,直线AB
射线:
把线段的一端无限延长,可以得到一条射线;
射线AB
射线有一个端点,直线没有端点。
线段:
用直尺把两点连接起来,就可以得到一条线段;线段是直线的一部分。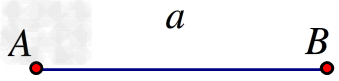
线段AB,线段a
线段有两个端点,它的长度是有限的,线段的长就是两点间的距离;
角:
从一点引出两条射线,就组成一个角。通常用符号“∠”来表示,角的大小看两条边叉开的大小,叉开的越大,角就越大。
角的大小与角两条边的长短没有关系。
角的计量单位:
角的计量单位是“度”,用符号“°”表示,把半圆分成180等份,每一份所对的角的大小是1度,记作1°。- 直线的性质:两点确定一条直线,直线长度是无限的
线段的性质:两点之间线段最短.
射线的性质:射线的长度是无限的 - 各种图线的表示方法:
直线:一个小写字母或两个大写字母.但前面必须加“直线”两字,如:直线l;直线m,直线AB;直线CD.
射线:一个小写字母或端点的大写字母和射线上的一个大写字母,前面必须加 “射线”两字.如:射线a;射线OA.
线段:用表示端点的大写字母表示,如线段AB;用一个小写字母表示,如线段a.
考点名称:轴对称,轴对称图形
- 如果一个图形沿着一条直线对折,直线两边的图形能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
学过的图形中,线段、角、等腰三角形、等边三角形、长方形、正方形、等腰梯形、圆形、扇形都是轴对称图形,各自有不同数目的对称轴。
考点名称:倒数
倒数定义:
乘积是1的两个数叫做互为倒数。
求法:
1.求一个分数的倒数,例如3/4,我们只须把3/4这个分数的分子和分母交换位置,即得3/4的倒数为4/3。
2.求一个整数的倒数,只须把这个整数看成是分母为1的分数,然后再按求分数倒数的方法即可得到。
如12,即12/1,再把12/1这个分数的分子和分母交换位置,把分子做分母,分母做分子,则有1/12。 即12倒数是1/12。
说明:倒数是本身的数是1和-1。(0没有倒数)
倒数的特点:一个正实数(1除外)加上它的倒数一定大于2。
考点名称:正比例的意义,反比例的意义
正比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线;
用字母表示为如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示: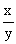 =k(一定);
=k(一定);
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变.正比例和反比例
反比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;
如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定)。- 反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
成反比例的量:
前提:两种相关的量(乘法关系)
要求:一个量变化,另一个量也随着变化,并且,这两个量中相对应的两个数的乘积一定。
结论:这两个量就叫做反比例的量,它们的关系叫做反比例关系。 正比例和反比例关系:
相同点:
①正比例和反比例都含有三个数量,在这三个数量中,均有一个定量、两个变量。
②在正、反比例的两个变量中,均是一个量变化,另一个量也随之变化。并且变化方式均属于扩大(乘以一个数)或缩小(除以一个数)若干倍的变化。
不同点:
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线;反比例是曲线。
③公式不同:正比例是(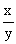 =k(一定)),反比例是(xy=k(一定))。
=k(一定)),反比例是(xy=k(一定))。
④规律不同:正比例是一个数缩小,另一个数也缩小,一个数扩大,另一个数也扩大;反比例是一个数缩小,另一个数就扩大,一个数扩大另一个数就缩小。- 判断两种量成正比例、反比例或不成比例的方法:
(1)找出两种相关联的量。
(2)根据两种相关联的量之间的关系列出数量关系式。
(3)如果两种量中相对应的两个数的比值(也就是商)一定,就是成正比例的量;若积一定,就是反比例的量。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |