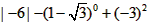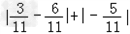已知a,b,c在数轴上的位置如下图所示:(1)求+-的值;(2)比较a+b,b+c,c-b的大小,并用“<将它们连接起来。-七年级数学
题文
| 已知a,b,c在数轴上的位置如下图所示: |
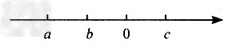 |
(1)求 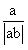 + +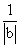 - -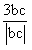 的值; 的值; (2)比较a+b,b+c,c-b的大小,并用“< 将它们连接起来。 |
答案
解:(1)原式=  (2)a+b<b+c<c-b。 |
据专家权威分析,试题“已知a,b,c在数轴上的位置如下图所示:(1)求+-的值;(2)比较a+b,..”主要考查你对 有理数的加减混合运算,数轴,比较有理数的大小 等考点的理解。关于这些考点的“档案”如下:
有理数的加减混合运算数轴比较有理数的大小
考点名称:有理数的加减混合运算
- 有理数的加减运算顺序:
同级运算从左往右(从左往右算)
异级运算先二后一(先算二级运算,再算一级运算,×、 ÷为二级,+、 -为一级)
有括号的先里后外(先算括号里的,再算括号外的) - 有理数加减混合运算的步骤:
(1)把减法转化为加法,写成省略加号和括号的形式;
(2)应用加法的交换律与结合律,简化运算;
(3)求出结果。 有理数加减混合运算:
有理数加法运算总是涉及两个方面:一方面是确定结果的符号,另一方面是求结果的绝对值。
法则:
(一)同号两数相加,取相同的符号,并把绝对值相加。
(二)异号两数相加,绝对值相等时和为0,绝对值不等时,取绝对值较大数的符号,并用较大的绝对值减去较小的绝对值。
(三)一个数同0相加,仍得这个数。
步骤:
①减法化加法
②省略加号和括号
③运用加法法则,加法运算律进行简便运算。有理数减法法则:
减去一个数,等于加上这个数的相反数。
注:
在运用减法法则时,注意两个符号的变化,
一是运算符号,减号变成加号,
二是性质符号,减数变成它的相反数。
有理数的加减混合运算加减混合运算可以通过减法法则,将减法化加法,统一为加法运算。
考点名称:数轴
- 数轴定义:
规定了唯一的原点,正方向和单位长度的一条直线叫做数轴。
数轴具有三要素:
原点、正方向和单位长度,三者缺一不可。
数轴是直线,可以向两方无限延伸,因此所有的有理数都可用数轴上的点来表示。 - 用数轴上的点表示有理数:
每一个有理数都可用数轴上的点来表示,表示正数的点在数轴原点的右边,表示负数的点在数轴原点的左边,原点表示数0。
1.数轴上的点表示的数不一定都是有理数,还可能是无理数,但有理数都可用数轴上的点来表示。
2.表示正数的点都在原点右边,表示负数的点都在原点左边。
3.数轴上的点表示的数,右边的点表示的数总比左边的点表示的数大,因此,可借助数轴比较有理数的大小。 - 数轴的画法:
1.画一条直线(一般画成水平的直线);
2.在直线上根据需要选取一点为原点(在原点下面标上“0”);
3.确定正方向(一般规定向右为正,并用箭头表示出来);
4.选取适当的长度为单位长度,
从原点向右,每隔一个单位长度取一点,依次表示1,2,3,…;
从原点向左,用类似的方法依次表示-1,-2,-3,…。 数轴的应用范畴:
符号相反的两个数互为相反数,零的相反数是零。(如2的相反—2)
在数轴上离开原点的距离就叫做这个数的绝对值。一个正数的绝对值是它本身,一个负数的相反数是它的正数,0的绝对值是0。
考点名称:比较有理数的大小
- 比较有理数大小的方法:
有理数是整数和分数的统称,一切有理数都可以化成分数的形式。
数轴法:
1、在数轴上表示的两个数,右边的总比左边的数大。
2、正数都大于零,负数都小于零,正数大于负数。
绝对值法:
1、两个正数比较大小,绝对值大的数大;
2、两个负数比较大小,绝对值大的数反而小。
差值法:
设a、b为任意两有理数,两数做差,若a-b>0,则a>b ; 若a-b<0则a<b
商值比较法:
设a、b为任意两有理数,两数做商,若a/b>1,则a>b;若a/b<1,则a<b
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![下列各式中正确的是[]A.-6-(-3)=-9B.+6-(-5)=1C.-7-7=0D.+4-(+6)=-2-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/10/2019-02-17/9a057928b5bd620b62e54ac2e5a92210.png)
![阅读理解:计算:(﹣5)+(﹣9)+17+(﹣3)解析:因为,,,,原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]=[(一5)+(﹣9)+17+(一3)]+[(﹣)+(﹣)++(﹣)]=0+(﹣1)=﹣1上面这种计算方法叫折项法-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/10/2019-02-17/ccd817fd912b24cd27f9e10f25ed892c.png)