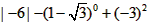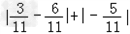Forrealnumbera,let[a]denotethemaximumintegerwhichdoesnotexceeda.Forexample,[3.1]=3,[-1.5]=-2,[0.7]=0Nowletf(x)=(x+1)/(x-1),then[f(2)]+[f(3)]+…+[f(100)]=_-数学
题文
| For real number a,let[a]denote the maximum integer which does not exceed a.For example,[3.1]=3,[-1.5]=-2,[0.7]=0 Now let f(x)=(x+1)/(x-1),then[f(2)]+[f(3)]+…+[f(100)]=______.(英汉小词典real number:实数;the maximum integer which does not exceed a:不超过a的最大整数) |
答案
∵f(x)=
∴f(2)=
f(4)=
∴[f(2)]=3,[f(3)]=2,[f(4)]=[f(5)]=…[f(100)]=1, ∴[f(2)]+[f(3)]+…+[f(100)], =3+2+1+…+1, =5+1×97, =102. 故答案为:102. |
据专家权威分析,试题“Forrealnumbera,let[a]denotethemaximumintegerwhichdoesnotexc..”主要考查你对 有理数的加减混合运算 等考点的理解。关于这些考点的“档案”如下:
有理数的加减混合运算
考点名称:有理数的加减混合运算
- 有理数的加减运算顺序:
同级运算从左往右(从左往右算)
异级运算先二后一(先算二级运算,再算一级运算,×、 ÷为二级,+、 -为一级)
有括号的先里后外(先算括号里的,再算括号外的) - 有理数加减混合运算的步骤:
(1)把减法转化为加法,写成省略加号和括号的形式;
(2)应用加法的交换律与结合律,简化运算;
(3)求出结果。 有理数加减混合运算:
有理数加法运算总是涉及两个方面:一方面是确定结果的符号,另一方面是求结果的绝对值。
法则:
(一)同号两数相加,取相同的符号,并把绝对值相加。
(二)异号两数相加,绝对值相等时和为0,绝对值不等时,取绝对值较大数的符号,并用较大的绝对值减去较小的绝对值。
(三)一个数同0相加,仍得这个数。
步骤:
①减法化加法
②省略加号和括号
③运用加法法则,加法运算律进行简便运算。有理数减法法则:
减去一个数,等于加上这个数的相反数。
注:
在运用减法法则时,注意两个符号的变化,
一是运算符号,减号变成加号,
二是性质符号,减数变成它的相反数。
有理数的加减混合运算加减混合运算可以通过减法法则,将减法化加法,统一为加法运算。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![下列各式中正确的是[]A.-6-(-3)=-9B.+6-(-5)=1C.-7-7=0D.+4-(+6)=-2-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/10/2019-02-17/9a057928b5bd620b62e54ac2e5a92210.png)
![阅读理解:计算:(﹣5)+(﹣9)+17+(﹣3)解析:因为,,,,原式=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]=[(一5)+(﹣9)+17+(一3)]+[(﹣)+(﹣)++(﹣)]=0+(﹣1)=﹣1上面这种计算方法叫折项法-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/10/2019-02-17/ccd817fd912b24cd27f9e10f25ed892c.png)