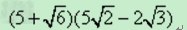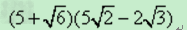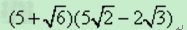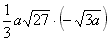题文

计算： （1）( 3 8 -3 3 )- 6 （2）2 12 +3 1 1 3 - 5 1 3 - 2 3 48 （3） 2 +1+ 3 ( 3 - 6 )+ 8 ； （4）9 45 ÷ 2 1 2 × 3 2 2 2 3 （5） 3a2 ÷3 a 2 × 1 2 2a 3 ．

题型：解答题  难度：中档

答案

（1）原式= 8 3 × 6 -3 3 × 6 = 8 3 ×6 -3 3 × 3 × 2 = 3 2 -9 2 ； （2）原式=4 3 +3× 2 3 3 - 4 3 3 - 8 3 3 =2 3 ； （3）原式= 2 +1+3-3 2 +2 2 =4； （4）原式=27 5 ÷ 5 2 × 3 2 8 3 =27× 3 2 5÷ 5 2 × 8 3 = 162 3 3 ； （5）原式=1× 1 3 × 1 2 3a2÷ a 2 × 2a 3 = 1 6 × 4a2 = a 3 ．

据专家权威分析，试题“计算：（1）(38-33)-6（2）212+3113-513-2348（3）2+1+3(3-6)+8；（4）945..”主要考查你对  二次根式的加减乘除混合运算，二次根式的化简  等考点的理解。关于这些考点的“档案”如下：

二次根式的加减乘除混合运算，二次根式的化简

考点名称：二次根式的加减乘除混合运算，二次根式的化简

• 二次根式的加减乘除混合运算：
  顺序与师叔运算的顺序一样,先乘方，后乘除，最后算加减，有括号的先算括号内的。
  ①在运算过程中,多项式乘法,乘法公式和有理数(式)中的运算律在二次根式的运算中仍然适用。
  ②二次根式的加减乘除混合运算过程中，每个根式可以看作是一个“单项式”，多个不同类的二次根式的和可以看作“多项式”。
  ③运算结果是根式的，一般应表示为最简二次根式。
  二次根式的化简：
  先对分子、分母因式分解，能约分的就约分，能开方的就开方，或先对被开方数进行通分，然后再通过分母有理化进行化简。
  

• 二次根式混合运算掌握：
  1、确定运算顺序。
  2、灵活运用运算定律。
  3、正确使用乘法公式。
  4、大多数分母有理化要及时。
  5、在有些简便运算中也许可以约分，不要盲目有理化。
  6、字母运算时注意隐含条件和末尾括号的注明。
  7、提公因式时可以考虑提带根号的公因式。

  二次根式化简方法：
  二次根式的化简是初中阶段考试必考的内容，初中竞赛的题目中也常常会考察这一内容。
  分母有理化：
  分母有理化即将分母从非有理数转化为有理数的过程，以下列出分母有理化的几种方法：
  （1）直接利用二次根式的运算法则：
  例：
  （2）利用平方差公式：
  例：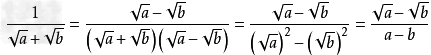
  （3）利用因式分解：
  例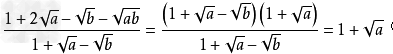：（此题可运用待定系数法便于分子的分解）
  
  换元法（整体代入法）：
  换元法即把根式中的某一部分用另一个字母代替的方法，是化简的重要方法之一。
  例：在根式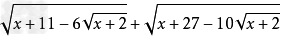中，令，即可得到
  原式=√(u2+9-6u)+√(u2+25-10u)=√(u-3)2+√(u-5)2=2u-8=2√(x+2)-8

  提公因式法：
  例：计算
  
  
  巧构常值代入法：
  例：已知x²-3x+1=0,求的值。
  分析：已知形如ax²+bx+c=0（x≠0）的条件，所求式子中含有的项，可先将ax²+bx+c=0化为x+=，即先构造一个常数，再代入求值。
  解：显然x≠0，x²-3x+1=0化为x+=3。
  原式==2.