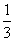掷两枚硬币,规定落地后,国徽朝上为正,国徽朝下为“反”,则会出现以下三种情况.分别求出每种情况的概率.(1)小刚做法:通过列表可知,每种情况都出现一次,因此各种情况发生的-数学
题文
掷两枚硬币,规定落地后,国徽朝上为正,国徽朝下为“反”,则会出现以下三种情况. 分别求出每种情况的概率. (1)小刚做法:通过列表可知,每种情况都出现一次,因此各种情况发生的概率均占
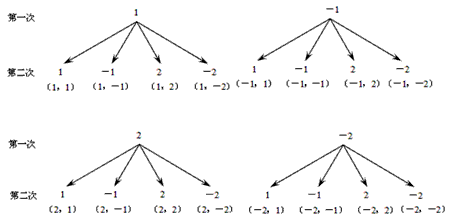
 小涵的作法:  小敏的做法:  通过以上列表,小敏得出:“正正”的情况发生概率为
(1)以上三种做法,你同意哪种,说明你的理由. (2)用列表法求概率时要注意哪些? |

 。
。 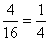
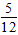
![有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面,则钥匙藏在黑色瓷砖下面的概率是[]A、B、C、D、-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/114/2019-05-19/1f98957f1a502bb89c7421e326170484.gif)