濮樺瓨妲搁惇鍏煎皾濡亷绱濈仦杈ㄦЦ閻鍢查懕姘モ偓鍌涱儘闂傤喛顢戞禍鍝勫箵闁綀绔熼敍鐔烘箒閻偐娉╅惄鍫濐槱閵嗗倹澧犳慨瀣偓浣规К瑜版帪绱濋崣鍫モ偓浣告偘瑜版帒骞撻妴鍌濆閸掔増鐫欓崡妤勫垁娑撳﹥妲敍灞藉磮娑撳洤鎷伴弰銉ょ秶閵嗭拷
已知抛物线y=k(x+1)(x-3k)与x轴交于点A,B,与y轴交于点C,且△ABC是以AC为腰的等腰三角形.求k的值.-数学
题文
已知抛物线y=k(x+1)(x-
|
答案
| 根据题意,得C(0,-3). 令y=0,则k(x+1)(x-
x=-1或x=
设A点的坐标为(-1,0),则B(
①当AC=BC时, OA=OB=1, B点的坐标为(1,0),
k=3; ②当AC=AB时,点B在点A的右面时, ∵AC=
则AB=AC=
B点的坐标为(
k=
③当AC=AB时,点B在点A的左面时, B点的坐标为(-
k=
综上所述,符合条件的k的值有:k=3,k=
|

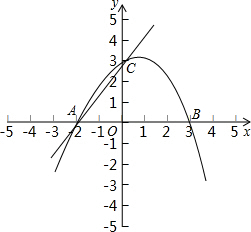


![根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是[]A.6<x<6.17B.6.17<x<6.18C.6.18-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/121/2019-12-17/d9417b49137e833b3ed6b7c2f391cbf0.gif)



