抛物线y=12x2-2(m+54)x+2(m+1)与y轴的正半轴交于点C,与x轴交于A、B两点,并且点B在A的右边,△ABC的面积是△OAC面积的3倍.(1)求这条抛物线的解析式;(2)判断△OBC与△OCA是否相-数学
题文
抛物线y=
(1)求这条抛物线的解析式; (2)判断△OBC与△OCA是否相似,并说明理由. |
答案
(1)设A(x1,0),(x2,0),△=4(m+
则2m+2>0,即m>-1, 又x1+x2=4(m+
x1x2=4(m+1)>0, ∴x2>x1>0, 由S△ABC=3S△OAC得S△OBC=4S△OAC, ∴x2=4x1, 与根与系数的关系联立可得,(
解得,m1=0,m2=-
对应的抛物线解析式为y=
(2)当m=0时,抛物线解析式为y=
可得A(1,0),B(4,0),C(0,2). 故
故△AOC∽△COB. 当m=-
可得A( |

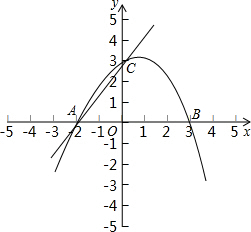


![根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是[]A.6<x<6.17B.6.17<x<6.18C.6.18-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/121/2019-12-17/d9417b49137e833b3ed6b7c2f391cbf0.gif)

