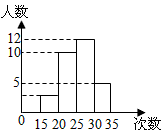
为了了解八年级学生一分钟跳绳次数的情况,某校抽取了一部分学生进行一分钟跳绳次数的测试,将所得数据进行处理,可得频数分布表:(1)在这个问题中,总体是______,样本容量a-七年级数学
题文
| 为了了解八年级学生一分钟跳绳次数的情况,某校抽取了一部分学生进行一分钟跳绳次数的测试,将所得数据进行处理,可得频数分布表: |
|
|
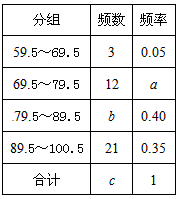
| (1)在这个问题中,总体是______,样本容量a=______; (2)第五小组的频数b=______,频率c=______; (3)若次数在110次以上(含110次)为达标,试估计该校八年级学生一分钟跳绳次数的达标率是多少? |
答案
| 解:(1)八年级学生一分钟跳绳次数的全体;100; (2)6;0.06; (3)93%。 |
据专家权威分析,试题“为了了解八年级学生一分钟跳绳次数的情况,某校抽取了一部分学生..”主要考查你对 频数与频率,总体、个体、样本、样本容量,用样本估算总体 等考点的理解。关于这些考点的“档案”如下:
频数与频率总体、个体、样本、样本容量用样本估算总体
考点名称:频数与频率
- 频数:一般我们称落在不同小组中的数据个数为该组的频数。
频率:频数与数据总数的比值为频率。频率反映了各组频数的大小在总数中所占的分量。 频数:
在一组依大小顺序排列的测量值中,当按一定的组距将其分组时出现在各组内的测量值的数目。
如有一组测量数据,数据的总个数N=148最小的测量值xmin=0.03,最大的测量值xmax=31.67,按组距为△x=3.000将148个数据分为11组,其中分布在15.05~18.05范围内的数据有26个,则称该数据组的频数为26。频率:
如在314159265358979324中,‘9’出现的频数是3,出现的频率是3/18=16.7%
频数也称“次数”,对总数据按某种标准进行分组,统计出各个组内含个体的个数。而频率则每个小组的频数与数据总数的比值。
在变量分配数列中,频数(频率)表明对应组标志值的作用程度。
频数(频率)数值越大表明该组标志值对于总体水平所起的作用也越大,反之,频数(频率)数值越小,表明该组标志值对于总体水平所起的作用越小。
考点名称:总体、个体、样本、样本容量
- 掌握总体、个体、样本,样本容量的概念,能正确区分总体、个体、样本、样本容量
总体、个体、样本、样本容量,这四个概念之间其实有其内在联系,
总体:我们把所要考察的对象的全体叫做总体;
个体:把组成总体的每一个考察对象叫做个体;
样本:从总体中取出的一部分个体叫做这个总体的一个样本;
样本容量:一个样本包含的个体的数量叫做这个样本的容量。
我们在区分这四个概念时,首先找出考察的对象,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量。
考点名称:用样本估算总体
- 用样本估计总体的两个手段:
(1)用样本的频率分布估计总体的分布;
(2)用样本的数字特征估计总体的数字特征,需要从总体中抽取一个质量较高的样本,才能不会产生较大的估计偏差,且样本的容量越大,估计的结果也就越精确。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |


![某地区去年10月下旬各天的最低气温依次是(单位:摄氏度)-7,-6,-8,-8,-6,-5,-6,-8,-7,-6,则出现次数最多的气温频率是[]A.0.25B.0.1C.0.2D.0.4-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/124/2019-12-18/830004411a90f8d5aa4c230811aed863.jpg)
