振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方-九年级数学
题文
| 振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3︰4︰5︰8︰6,又知此次调查中捐款25元和30元的学生一共42人。 |
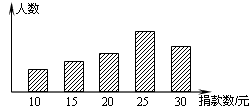 |
| (1)他们一共调查了多少人? (2)这组数据的众数、中位数各是多少? (3)若该校共有1560名学生,估计全校学生捐款多少元? |
答案
| 解:(1)设捐款30元的有6x人,则8x+6x=42 ∴ x=3 ∴ 捐款人数共有:3x+4x+5x+8x+6x=78(人)。 (2)由图象可知:众数为25(元);由于本组数据的个数为78,按大小顺序排列处于中间位置的两个数都是25(元),故中位数为25(元)。 (3)全校共捐款:(9×10+12×15+15×20+24×25+18×30)× 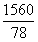 =34200(元)。 =34200(元)。 |
据专家权威分析,试题“振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿..”主要考查你对 条形图,中位数和众数 等考点的理解。关于这些考点的“档案”如下:
条形图中位数和众数
考点名称:条形图
- 条形图定义:
用一个单位长度表示一定的数量,根据数量的多少画成长短不同的条形,条形的宽度必须保持一致,然后把这些条形排列起来,这样的统计图叫做条形统计图。它可以表示出每个项目的具体数量。 条形图特点:
(1)能够显示每组中的具体数据;
(2)易于比较数据之间的差别。
描绘条形图的3要素:组数、组宽度、组限。
1.组数
把数据分成几组,指导性的经验是将数据分成5~10组。
2.组宽度
通常来说,每组的宽度是一致的。组数和组宽度的选择就不是独立决定的,一个经验标准是:
近似组宽度=(最大值-最小值)/组数
然后根据四舍五入确定初步的近似组宽度,之后根据数据的状况进行调整。
3.组限
分为组下限(进入该组的最小可能数据)和组上限(进入该组的最大可能数据),并且一个数据只能在一个组限内。
绘画条形图时,不同组之间是有空隙的;而绘画直方图时,不同组之间是没有空隙的。
使用条形图的情况:
轴标签过长;
显示的数值是持续型的。条形图具有下列图表子类型:
簇状条形图和三维簇状条形图 簇状条形图比较各个类别的值。在簇状条形图中,通常沿垂直轴组织类别,而沿水平轴组织数值。三维簇状条形图以三维格式显示水平矩形,而不以三维格式显示数据。堆积条形图和三维堆积条形图 堆积条形图显示单个项目与整体之间的关系。三维堆积条形图以三维格式显示水平矩形,而不以三维格式显示数据。
百分比堆积条形图和三维百分比堆积条形图 此类型的图表比较各个类别的每一数值所占总数值的百分比大小。三维百分比堆积条形图表以三维格式显示水平矩形,而不以三维格式显示数据。
水平圆柱图、圆锥图和棱锥图 水平圆柱图、圆锥图和棱锥图可以使用为矩形条形图提供的簇状图、堆积图和百分比堆积图,并且它们以完全相同的方式显示和比较数据。唯一的区别是这些图表类型显示圆柱、圆锥和棱锥形状而不是水平矩形。
- 制作条形图的步骤:
(1)根据统计资料整理数据,一般整理成表格形式;
(2)画出横轴、纵轴,确定它们所表示的项目,选定标尺,按一定比例作为长度单位,长短要适中,根据数据的大小对应标出;
(3)画直条,条形的高与数据的大小成比例。条形的宽度、间隔要一致;
(4)写上统计总标题、制图日期及数量单位。
考点名称:中位数和众数
- 中位数:一般地,n个数据按大小顺序排列,处于最中间位置的一个数据(或最中间位置的两个数据的平均数)叫这组数据的中位数。
众数:在一组数据中,出现次数最多的数据。 - 中位数的位置:
当样本数为奇数时,中位数=(N+1)/2;当样本数为偶数时,中位数为N/2与1+N/2的均值
众数性质:
用众数代表一组数据,可靠性较差,不过,众数不受极端数据的影响,并且求法简便。在一组数据中,如果个别数据有很大的变动,选择中位数表示这组数据的“集中趋势”就比较适合。
当数值或被观察者没有明显次序(常发生于非数值性资料)时特别有用,由于可能无法良好定义算术平均数和中位数。例子:{鸡、鸭、鱼、鱼、鸡、鱼}的众数是鱼。
众数算出来是销售最常用的,代表最多的
众数是在一组数据中,出现次数最多的数据
两组数据中,都是1,2出现次数最多
所以1,2是众数
众数:
一般来说,一组数据中,出现次数最多的数就叫这组数据的众数。
例如:1,2,3,3,4的众数是3。
但是,如果有两个或两个以上个数出现次数都是最多的,那么这几个数都是这组数据的众数。
例如:1,2,2,3,3,4的众数是2和3。
还有,如果所有数据出现的次数都一样,那么这组数据没有众数。
例如:1,2,3,4,5没有众数。
在高斯分布中,众数位于峰值。
平均数、中位数和众数的特征:
(1)平均数、中位数、众数都是表示一组数据“平均水平”的平均数。
(2)平均数能充分利用数据提供的信息,在生活中较为常用,但它容易受极端数字的影响,且计算较繁。
(3)中位数的优点是计算简单,受极端数字影响较小,但不能充分利用所有数字的信息。 中位数算出来可避免极端数据,代表着数据总体的中等情况。
(4)众数的可靠性较差,它不受极端数据的影响,求法简便,当一组数据中个别数据变动较大时,适宜选择众数来表示这组数据的“集中趋势”。 平均数、中位数和众数异同:
一、相同点
平均数、中位数和众数这三个统计量的相同之处主要表现在:都是来描述数据集中趋势的统计量;都可用来反映数据的一般水平;都可用来作为一组数据的代表。
二、不同点
它们之间的区别,主要表现在以下方面。
1、定义不同
平均数:一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数。
中位数:将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数 。
众数:在一组数据中出现次数最多的数叫做这组数据的众数。
2、求法不同
平均数:用所有数据相加的总和除以数据的个数,需要计算才得求出。
中位数:将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数是这组数据的中位数。它的求出不需或只需简单的计算。
众数:一组数据中出现次数最多的那个数,不必计算就可求出。
3、个数不同
在一组数据中,平均数和中位数都具有惟一性,但众数有时不具有惟一性。在一组数据中,可能不止一个众数,也可能没有众数。
4、呈现不同
平均数:是一个“虚拟”的数,是通过计算得到的,它不是数据中的原始数据。
中位数:是一个不完全“虚拟”的数。当一组数据有奇数个时,它就是该组数据排序后最中间的那个数据,是这组数据中真实存在的一个数据;但在数据个数为偶数的情况下,中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等,此时的中位数就是一个虚拟的数。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |