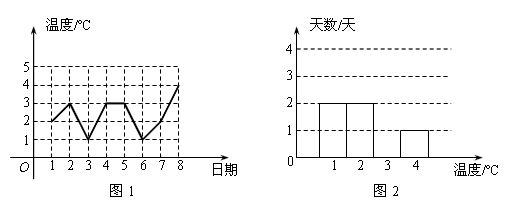
图1是某城市三月份1至8日的日最高气温随时间变化的折线统计图,小刚根据图1将数据统计整理后制成了图2。根据图中信息,解答下列问题:(1)将图2补充完整;(2)这8天的日最高气温-九年级数学
题文
| 图1是某城市三月份1至8日的日最高气温随时间变化的折线统计图,小刚根据图1将数据统计整理后制成了图2。 |
 |
|
根据图中信息,解答下列问题: |
答案
解:(1)补图如下: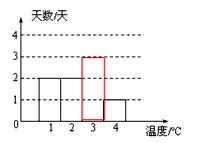 (2)2.5; (3) 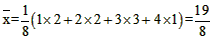 (℃)。 (℃)。 |
据专家权威分析,试题“图1是某城市三月份1至8日的日最高气温随时间变化的折线统计图,小..”主要考查你对 条形图,平均数,中位数和众数,折线图 等考点的理解。关于这些考点的“档案”如下:
条形图平均数中位数和众数折线图
考点名称:条形图
- 条形图定义:
用一个单位长度表示一定的数量,根据数量的多少画成长短不同的条形,条形的宽度必须保持一致,然后把这些条形排列起来,这样的统计图叫做条形统计图。它可以表示出每个项目的具体数量。 条形图特点:
(1)能够显示每组中的具体数据;
(2)易于比较数据之间的差别。
描绘条形图的3要素:组数、组宽度、组限。
1.组数
把数据分成几组,指导性的经验是将数据分成5~10组。
2.组宽度
通常来说,每组的宽度是一致的。组数和组宽度的选择就不是独立决定的,一个经验标准是:
近似组宽度=(最大值-最小值)/组数
然后根据四舍五入确定初步的近似组宽度,之后根据数据的状况进行调整。
3.组限
分为组下限(进入该组的最小可能数据)和组上限(进入该组的最大可能数据),并且一个数据只能在一个组限内。
绘画条形图时,不同组之间是有空隙的;而绘画直方图时,不同组之间是没有空隙的。
使用条形图的情况:
轴标签过长;
显示的数值是持续型的。条形图具有下列图表子类型:
簇状条形图和三维簇状条形图 簇状条形图比较各个类别的值。在簇状条形图中,通常沿垂直轴组织类别,而沿水平轴组织数值。三维簇状条形图以三维格式显示水平矩形,而不以三维格式显示数据。堆积条形图和三维堆积条形图 堆积条形图显示单个项目与整体之间的关系。三维堆积条形图以三维格式显示水平矩形,而不以三维格式显示数据。
百分比堆积条形图和三维百分比堆积条形图 此类型的图表比较各个类别的每一数值所占总数值的百分比大小。三维百分比堆积条形图表以三维格式显示水平矩形,而不以三维格式显示数据。
水平圆柱图、圆锥图和棱锥图 水平圆柱图、圆锥图和棱锥图可以使用为矩形条形图提供的簇状图、堆积图和百分比堆积图,并且它们以完全相同的方式显示和比较数据。唯一的区别是这些图表类型显示圆柱、圆锥和棱锥形状而不是水平矩形。
- 制作条形图的步骤:
(1)根据统计资料整理数据,一般整理成表格形式;
(2)画出横轴、纵轴,确定它们所表示的项目,选定标尺,按一定比例作为长度单位,长短要适中,根据数据的大小对应标出;
(3)画直条,条形的高与数据的大小成比例。条形的宽度、间隔要一致;
(4)写上统计总标题、制图日期及数量单位。
考点名称:平均数
- 平均数:
是指在一组数据中所有数据之和再除以数据的个数。平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标。
解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。
在统计工作中,平均数(均值)和标准差是描述数据资料集中趋势和离散程度的两个最重要的测度值。 - 平均数的分类:
(1)算术平均数:一般地,如果有n个数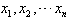 ,那么
,那么  ,叫做这n个数的算术平均数。
,叫做这n个数的算术平均数。
(2)加权平均数:一组数据 点的权分别为
点的权分别为 ,那么称
,那么称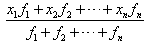 为这n个数的加权平均数。
为这n个数的加权平均数。
(3)样本平均数:样本中所有个体的平均数。
(4)总体平均数:总体中所有个体的平均数,统计学中常用样本的平均数估计总体的平均数。 平均数、中位数和众数关系:
联系:
平均数、中位数和众数都是来刻画数据平均水平的统计量,它们各有特点。对于平均数大家比较熟悉,中位数刻画了一组数据的中等水平,众数刻画了一组数据中出现次数最多的情况。
平均数非常明显的优点之一是,它能够利用所有数据的特征,而且比较好算。另外,在数学上,平均数是使误差平方和达到最小的统计量,也就是说利用平均数代表数据,可以使二次损失最小。因此,平均数在数学中是一个常用的统计量。但是平均数也有不足之处,正是因为它利用了所有数据的信息,平均数容易受极端数据的影响。
例如,在一个单位里,如果经理和副经理工资特别高,就会使得这个单位所有成员工资的平均水平也表现得很高,但事实上,除去经理和副经理之外,剩余所有人的平均工资并不是很高。这时,中位数和众数可能是刻画这个单位所有人员工资平均水平更合理的统计量。
中位数和众数这两个统计量的特点都是能够避免极端数据,但缺点是没有完全利用数据所反映出来的信息。
由于各个统计量有各自的特征,所以需要我们根据实际问题来选择合适的统计量。
当然,出现极端数据不一定用中位数,一般,统计上有一个方法,就要认为这个数据不是来源于这个总体的,因而把这个数据去掉。比如大家熟悉的跳水比赛评分,为什么要去掉一个最高分、一个最低分呢,就认为这两个分不是来源于这个总体,不能代表裁判的鉴赏力。于是去掉以后再求剩下数据的平均数。需要指出的是,我们处理的数据,大部分是对称的数据,数据符合或者近似符合正态分布。这时候,均值(平均数)、中位数和众数是一样的。区别:
只有在数据分布偏态(不对称)的情况下,才会出现均值、中位数和众数的区别。所以说,如果是正态的话,用哪个统计量都行。如果偏态的情况特别严重的话,可以用中位数。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |