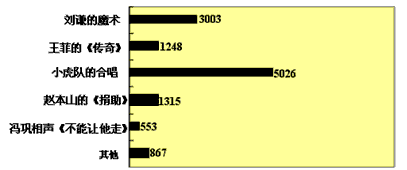
2010年春季以来,我国西南地区遭受了严重的旱情,某校学生会自发组织了“保护水资源从我做起”的活动.同学们采取问卷调查的方式,随机调查了本校150名同学家庭月人均用水量和节-七年级数学
区别:
只有在数据分布偏态(不对称)的情况下,才会出现均值、中位数和众数的区别。所以说,如果是正态的话,用哪个统计量都行。如果偏态的情况特别严重的话,可以用中位数。
除了需要刻画平均水平的统计量,统计中还有刻画数据波动情况的统计量。比如,平均数同样是5,它所代表的数据可能是1、3、5、7、9,可能是4、4.5、5、5.5、6。也就是说5所代表的不同组数据的波动情况是不一样的。怎样刻画数据的波动情况呢?很自然的想法就是用最大值减最小值,即求一组数据的极差。数学中还有方差、标准差等许多用来刻画数据特征的统计量。当然这些都是教师感兴趣、值得了解的内容,不是小学数学的教学要求。
(1)公式法:
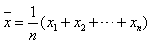 ;
; (2)加权平均数公式:
 。
。 考点名称:扇形图
- 定义:
用圆的面积代表事物总体,以扇形的面积和圆的面积的比值表示个项目占总体的百分数的统计图,叫做扇形统计图。 - 特点:
(1)用扇形的面积表示部分在总体中所占的百分比;
(2)易于显示每组数据相对于总数的大小。
作用:
能清楚地了解各部分数与总数之间的关系与比例。
扇形面积与其对应的圆心角的关系是:
扇形面积越大,圆心角的度数越大。
扇形面积越小,圆心角的度数越小。
扇形所对圆心角的度数与百分比的关系是:
圆心角的度数=百分比×360度
扇形统计图还可以画成圆柱形的。 - 制作扇形统计图的步骤:
(1)根据统计资料,整理数据,并计算出部分占整体的百分数;
(2)根据各部分占总体的百分数,计算出各部分扇形圆心角的度数;
(3)取适当半径作圆,按圆心角将圆分成几个扇形;
(4)对应标上各部分名称及占总体的百分数。
考点名称:用样本估算总体
- 用样本估计总体的两个手段:
(1)用样本的频率分布估计总体的分布;
(2)用样本的数字特征估计总体的数字特征,需要从总体中抽取一个质量较高的样本,才能不会产生较大的估计偏差,且样本的容量越大,估计的结果也就越精确。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:某中学准备搬迁新校舍,在迁入新校舍之前,同学们就该校学生如何到校问题进行了一次调查,并将调查结果制成了表格,条形图和扇形统计图,请你根据图表信息完成下列各题:(1)此-七年级数学
下一篇:小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:(1)请将表格补充完整;(2)请将条形统计图补充完整;(3)扇形统计图中,表示短信费的扇形的圆-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |