如图1是一副三角尺拼成的图案(1)求∠EBC的度数;(2)将图1中的三角尺ABC绕点B旋转α度(0°<α<90°)能否使∠ABE=2∠DBC?若能,求出∠EBC的度数;若不能,说明理由。(图2、图3供参考)-七年级数学
题文
| 如图1是一副三角尺拼成的图案 (1)求∠EBC的度数; (2)将图1中的三角尺ABC绕点B旋转α度(0°<α<90°)能否使∠ABE=2∠DBC?若能,求出∠EBC的度数;若不能,说明理由。(图2、图3供参考) |
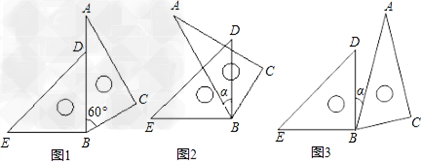 |
答案
| 解:(1)∠EBC=∠ABC+∠EBD=60°+90°=150°. (2)第一种情况:若逆时针旋转α度,如图2: 据题意得90°﹣α=2(60°﹣α), 得α=30°, ∴∠EBC=(90°﹣30°)+30°+(60°﹣30°)=120°, 第二种情况:若顺时针旋转度,如图3, 据题意得90°+α=2(60°+α), 得α=﹣30° ∵0<α<90°, α=﹣30°不合题意,舍去. 故∠EBC=∠120 °. |
据专家权威分析,试题“如图1是一副三角尺拼成的图案(1)求∠EBC的度数;(2)将图1中的三角..”主要考查你对 角的概念 ,图形旋转 等考点的理解。关于这些考点的“档案”如下:
角的概念 图形旋转
考点名称:角的概念
角的基本概念:
从静态角度认识角:由一个点出发的两条射线组成的图形叫角;
从动态角度认识角:一条射线绕着它的顶点旋转到另一个位置,则这两条射线组成的图像叫角。有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。
①因为射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边长无关。
②角的大小可以度量,可以比较。
③根据角的度数,角可以分为锐角、直角、钝角、平角、周角。
角的表示:角可以用大写英文字母、阿拉伯数字或小写的希腊字母表示,如∠1,∠α,∠BAD等。- 角的分类:
根据角的度数,角可以分为锐角、直角、钝角、平角、周角。
平角:180。的角,当角的两边在一条直线上时,组成的角叫做平角。即射线OA绕点O旋转,当终边在始边OA的反向延长线上时所成的角;
直角:90。的角,即线OA绕点O旋转,当终边与始边垂直时所成的角,平角的一半叫做直角;
锐角:大于0。小于90。的角,小于直角的角叫做锐角;
钝角:大于90。小于180。的角,大于直角且小于平角的角叫做钝角。
周角:360。的角,即射线OA绕点O旋转,当终边与始边重合时所成的角。
角的性质:
①角的大小与边的长短无关,只与构成角的两条射线的幅度大小有关;
②角的大小可以度量,可以比较;
③角可以参与运算。
角的度量:
角的度量有如下规定:把一个平角180等分,每一份就是1度的角,单位是度,用“。”,1度记作“1°”,n度记作“n°”。把1°的角60等分,每一份叫做1分的角,1分记作“1′”。把1′的角60等分,每一份叫做1秒的角,1秒记作“1″”。1°=60′=3600″。
考点名称:图形旋转
- 定义:
在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。
图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变。 - 图形旋转性质:
(1)对应点到旋转中心的距离相等。
(2)对应点与旋转中心所连线段的夹角等于旋转角。
旋转对称中心
把一个图形绕着一个点旋转一定的角度后,与原来的图形相吻合,这种图形叫做 旋转对称图形,这个定点叫做 旋转对称中心,旋转的角度叫做 旋转角。(旋转角大于0°小于360°)
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![图中小于平角的角有()个.[]A.5B.6C.7D.8-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/138/2020-01-01/2f6e2150987751eb29aa5d140f64abda.png)


![钟表上为4点整时,秒针与分针和分针与时针之间的夹角分别为[]A.0°和90°B.105°和0°C.90°和105°D.0°和120°-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/138/2019-12-31/a5c3e2e9f387fcbbaa70123e5524ae9b.png)
