如图1,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上,(1)试找出∠1,∠2,∠3之间的等式关系,并说明理由;(2)应用(1)的结论解下列问题①如图2,A点在B处北偏东-数学
题文
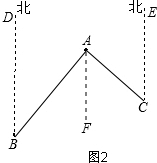
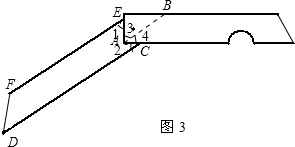
| 如图1,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上, (1)试找出∠1,∠2,∠3之间的等式关系,并说明理由; (2)应用(1)的结论解下列问题 ①如图2,A点在B处北偏东40°方向,A点在C处的北偏西45°方向,求∠BAC的度数? ②在图3中,小刀的刀片上、下是∥的,刀柄外形是一个直角梯形(下底挖去一小半圆),求∠1+∠2的度数? 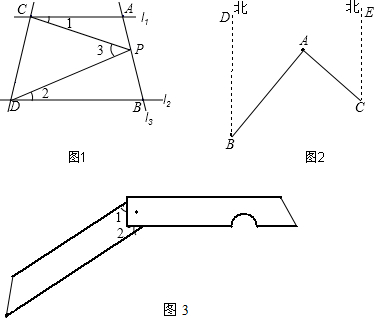 |

![图中小于平角的角有()个.[]A.5B.6C.7D.8-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/138/2020-01-01/2f6e2150987751eb29aa5d140f64abda.png)


![钟表上为4点整时,秒针与分针和分针与时针之间的夹角分别为[]A.0°和90°B.105°和0°C.90°和105°D.0°和120°-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/138/2019-12-31/a5c3e2e9f387fcbbaa70123e5524ae9b.png)
