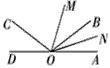
(1)如图,OM平分∠AOC,ON平分∠BOC.①填空:∠MON=∠MOC﹣∠_________;②如果∠AOB=90°,∠BOC=30°,求∠MON的度数;③如果∠AOB=α,∠BOC=θ,求∠MON的度数,从结果你能看出∠MON与∠AOB有什-七年级数学
题文
| (1)如图,OM平分∠AOC,ON平分∠BOC. ①填空:∠MON=∠MOC﹣∠ _________ ; ②如果∠AOB=90°,∠BOC=30°,求∠MON的度数; ③如果∠AOB=α,∠BOC=θ,求∠MON的度数,从结果你能看出∠MON与∠AOB有什么关系? (2)知识迁移:线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法,请你模仿(1)中的第③小题,设计一道以线段为背景的计算题,并直接写出其中的关系来(不必写出解答过程). |
|
|
答案
| 解:(1)①NOC; ②∵∠AOB=90°,∠BOC=30° ∴∠AOC=∠AOB+∠BOC=120° ∵OM平分∠AOC ∴∠MOC=  ∠AOC=60°(角平分线的定义) ∠AOC=60°(角平分线的定义)同理,∠NOC=  ∠BOC=15° ∠BOC=15°∴∠MON=∠MOC﹣∠NOC=60°﹣15°=45°; ③∵∠AOB=α,∠BOC=θ ∴∠AOC=∠AOB+∠BOC=α+θ ∵OM平分∠AOC(已知) ∴∠MOC=  ∠AOC= ∠AOC= (α+θ)(角平分线的定义) (α+θ)(角平分线的定义)同理,∠NOC=  ∠BOC= ∠BOC= θ θ∴∠MON=∠MOC﹣∠NOC=  (α+θ)﹣ (α+θ)﹣ θ= θ= α α∠MON与∠AOB的关系为:∠MON=  ∠AOB. ∠AOB.(2)如图,  B是线段AC上一点,M是线段AC的中点,N是线段BC的中点,AB=a,BC=b,求出线段MN的长度. 则得到关系:MN=  AB. AB. |
据专家权威分析,试题“(1)如图,OM平分∠AOC,ON平分∠BOC.①填空:∠MON=∠MOC﹣∠_________;..”主要考查你对 余角,补角,直线,线段,射线 等考点的理解。关于这些考点的“档案”如下:
余角,补角直线,线段,射线
考点名称:余角,补角
余角:
如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A
补角:
如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角
∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A- 补角的性质:
同角的补角相等。比如:∠A+∠B=180°,∠A+∠C=180°,则:∠C=∠B。
等角的补角相等。比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D则:∠C=∠B。
余角的性质:
同角的余角相等。比如:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B。
等角的余角相等。比如:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B。
注意:
①钝角没有余角;
②互为余角、补角是两个角之间的关系。如∠A+∠B+∠C=90°,不能说∠A、∠B、∠C互余;同样:如∠A+∠B+∠C=180°,不能说∠A、∠B、∠C互为补角;
③互为余角、补角只与角的度数相关,与角的位置无关。只要它们的度数之和等于90°或180°,就一定互为余角或补角。 - 余角与补角概念认识提示:
(1)定义中的“互为”一词如何理解?
如果∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 , 同样∠2的补角是∠1。
(2)互余、互补的两角是否一定有公共顶点或公共边?
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
考点名称:直线,线段,射线
- 基本概念:
直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。一条直线可以用一个小写字母表示。
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。一条线段可用它的端点的两个大写字母来表示。
射线:直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。一条射线可以用端点和射线上另一点来表示。
注意:
①线和射线无长度,线段有长度。
②直线无端点,射线有一个端点,线段有两个端点。 直线、射线、线段的基本性质:
图形 表示法 端点 延长线 能否度量 基本性质 直线 没有端点的一条线 一条线,
不要端点无 可以向两边无限延长 否 两端都没有端点,可以无限延长,不可测量的线 射线 只有一个端点的一条线 一条线,
只有一边有端点一个 可以向一边无限延长 否 一端有端点,可以向一边无限延长,不可测量的线 线段 两边都有端点的一条线 一条线,两边都有端点 两个 不能延长 能 两端都有端点,不能延长,可测量的线 - 最新内容
- 相关内容
- 网友推荐
- 图文推荐
- 如图,已知AB,CD相交于O点,OE⊥A(2019-12-31)
- 如图,AOB为一直线,∠AOD:∠DOB=(2019-12-31)
- 如图,AB∥CD,AC⊥BC,图中与∠CAB(2019-12-31)
- 如图,∠AOC和∠DOB都是直角。(1)(2019-12-31)
- 如图,∠AOB=∠COD=90°,∠BOC=42(2019-12-31)
- 如图,Rt△ABC中,∠C=90°,CD⊥A(2019-12-31)
- ∠1,∠2互为补角,∠1<∠2,则∠(2019-12-31)
- 下列说法:①两条直线相交,有公共顶(2019-12-31)
- 如图,点O在直线AE上,OB平分∠AOC(2019-12-31)
- 若∠1=55°,则∠1的余角是()度.-七年级数学
- 如图,已知线段AB=20cm,C为直线AB上一点,且BC=4cm,
- 阅读:在用尺规作线段等于线段时,小明的具体做法如下
- 75°12′的余角等于()度。-七年级数学
- 下列命题:①两条直线相交,一角的两邻补角相等,则这
- 已知∠A=51°23',则∠A的余角的度数是()-七年级数学
- 如图,下列说法中的是[]A、直线AC经过点AB、射线DE与直
- 已知∠A=40°,则∠A的余角等于()度.-七年级数学
- 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远
- 下列说法中,正确的是[]A.一个角的补角必是钝角B.两
- 如图,已知AB和CD相交于点O,OE⊥A(2019-12-31)
- 已知∠1=30°,则∠1的余角度数是[(2019-12-31)
- 已知∠1=120°,则它的补角等于___(2019-12-31)
- 如图,OD平分∠BOC,OE平分∠AOC.(2019-12-31)
- 如果∠α和∠β互补,且∠α>∠β,(2019-12-31)
- 一个角比它的补角的一半还小27°,(2019-12-31)
- 以下3个说法中:①在同一直线上的4(2019-12-31)
- 一个角的余角比它的2倍角的补角还少(2019-12-31)
- 一个角是70°29′,则这个角的余角(2019-12-31)
- 一个角的补角比它的余角的3倍还大3(2019-12-31)
上一篇:下列说法中,正确的是[]A.一个角的补角必是钝角B.两个锐角一定互为余角C.直角没有补角D.如果∠MON=180°,那么M,O,N三点在一条直线上-七年级数学 下一篇:已知∠A=50°,则∠A的补角是()度-七年级数学零零教育社区:论坛热帖子[家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) [教师分享] 给远方姐姐的一封信 (2018-11-07) [教师分享] 伸缩门 (2018-11-07) [教师分享] 回家乡 (2018-11-07) [教师分享] 是风味也是人间 (2018-11-07) [教师分享] 一句格言的启示 (2018-11-07) [教师分享] 无规矩不成方圆 (2018-11-07) [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) [教师分享] 贪玩的小狗 (2018-11-07) [教师分享] 未命名文章 (2018-11-07)




![以下3个说法中:①在同一直线上的4点A、B、C、D可以表示5条不同的线段;②大于90°的角叫做钝角;③同一个角的补角一定大于它的余角.错误说法的个数有[]A.0个B.1个C.2个D.3个-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/140/2020-01-01/c8754480b07973e239a75a738c606434.png)