（6分）十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：小-八年级数学
题文
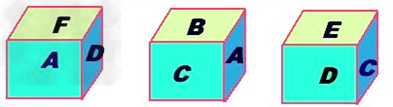
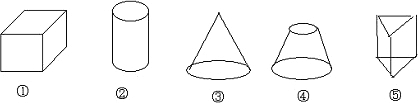
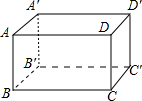
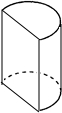
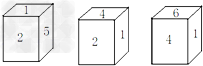
（6分）十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F ）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题： 小题1:（1）根据上面多面体模型，完成表格中的空格：
小题3:（3）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是 小题4:（4）某个玻璃鉓品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表三角形的个数为x个，八边形的个数为y个，x+y= |
答案
小题1:（1）20 12 30 小题2:（2）V+F-E=2 小题3:（3）20 小题4:（4）14 |
| 略 |
据专家权威分析，试题“（6分）十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数..”主要考查你对 认识立体几何图形，几何体的展开图，几何体的表面积，体积，截一个几何体 等考点的理解。关于这些考点的“档案”如下：
认识立体几何图形几何体的展开图几何体的表面积，体积截一个几何体
考点名称：认识立体几何图形
- 立体几何图形：
从实物中抽象出来的各种图形，统称为几何图形，几何图形是数学研究的主要对象之一。有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各个部分不都在同一平面内，它们是立体图形。由一个或多个面围成的可以存在于现实生活中的三维图形。点动成线，线动成面，面动成体。即由面围成体，看一个体最多看到立体图形实物三个面。 - 常见立体几何图形及性质:
①正方体:
有8个顶点，6个面。每个面面积相等（或每个面都有正方形组成）。有12条棱，每条棱长的长度都相等。（正方体是特殊的长方体）
②长方体:
有8个顶点，6个面。每个面都由长方形或相对的一组正方形组成。有12条棱，相对的4条棱的棱长相等。
③圆柱:
上下两个面为大小相同的圆形。有一个曲面叫侧面。展开后为长方形或正方形或平行四边形。有无数条高，这些高的长度都相等。
④圆锥:
有1个顶点，1个曲面，一个底面。展开后为扇形。只有1条高。四面体有1个顶点，四面六条棱高。
⑤直三棱柱：
三条侧棱切平行，上表面和下表面是平行且全等的三角形。
⑥球：
球是生活中最常见的图形之一，例如篮球、足球都是球，球是由一个面所围成的几何体。 - 常见的立体几何图形视图：
