阅读并探究下列问题:(1)如图1,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?为什么?(2)如图2,将长方形纸片剪四刀,其中AB∥CD,则∠2+∠4与∠1+∠3+∠5有何关系?为什么-七年级数学
题文
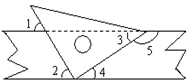
阅读并探究下列问题: (1)如图1,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?为什么? (2)如图2,将长方形纸片剪四刀,其中AB∥CD,则∠2+∠4与∠1+∠3+∠5有何关系?为什么? (3)如图3,将长方形纸片剪n刀,其中AB∥CD,你又有何发现? (4)如图4,直线AB∥CD,∠EFA=30.,∠FGH=90.,∠HMN=30.,∠CNP=50., 则∠GHM= .  |
答案
| 解: (1)图1中,∠2=∠1+∠3.理由如下: 过E点作EF∥AB,如图, 则EF∥CD, ∴∠AEF=∠1,∠CEF=∠3, ∴∠2=∠1+∠3 (2)图2中,分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB, 同(1)的证明方法一样可得∠2+∠4=∠1+∠3+∠5; (3)图3中,开口向左的角的度数的各等于开口向右的角的度数的和. (4)图4中,由(3)的结论得,∠BFG+∠GHM+∠MND=∠FGH+∠HMN, ∴30°+∠GHM+50°=90°+30°, ∴∠GHM=40°. 故答案为40°. |
| (1)过E点作EF∥AB,则EF∥CD,根据两直线平行,内错角相等得到∠AEF=∠1,∠CEF=∠3,即有∠2=∠1+∠3; (2)分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,根据两直线平行,内错角相等,同(1)一样易得到∠2+∠4=∠1+∠3+∠5; (3)综合(1)(2)易得开口向左的角的度数的各等于开口向右的角的度数的和. (4)利用(3)的结论得到∠BFG+∠GHM+∠MND=∠FGH+∠HMN,易计算出∠GHM. |
据专家权威分析,试题“阅读并探究下列问题:(1)如图1,将长方形纸片剪两刀,其中AB∥CD,..”主要考查你对 点、线、面、体 等考点的理解。关于这些考点的“档案”如下:
点、线、面、体
考点名称:点、线、面、体
- 点动成线,线动成面,面动成体:
长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体。
包围着体的是面,面有平的面和曲的面两种。
夜晚流星划过天空时留下一道明亮的光线,节日的焰火画出的曲线组成优美的图案,这些都给我们以线的形象,面和面相交的地方形成线。
天上的星星、世界地图上的城市等都给我们以点的形象,线和线相交的地方是点。
几何图形都是由点、线、面、体组成的,点是构成图形的基本元素。 - 常见几何体的三视图:


- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |