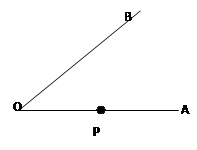如图l,已知∠AOC=m°,∠BOC=n°且m、n满足等式|3m-420|+(2n-40)2=0,射线OP从OB处绕点0以4度/秒的速度逆时针旋转.(1)试求∠AOB的度数;(2)如图l,当射线OP从OB处绕点O开始逆时针-七年级数学
题文
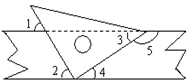
如图l,已知∠AOC=m°,∠BOC=n°且m、n满足等式|3m-420|+(2n-40)2=0,射线OP从OB处绕点0以4度/秒的速度逆时针旋转.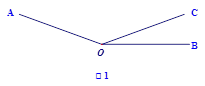 (1)试求∠AOB的度数; (2)如图l,当射线OP从OB处绕点O开始逆时针旋转,同时射线OQ从OA处以l度/秒的速度绕点0顺时针旋转,当他们旋转多少秒时,使得∠POQ=10°? (3)如图2,若射线OD为∠AOC的平分线,当射线OP从OB处绕点O开始逆时针旋转,同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转,使得这两条射线重合于射线OE处(OE在∠DOC的内部)时,且  = = ,试求x. ,试求x. |
答案
| (1)160°;(2)30秒或34秒;(3)2 |
试题分析:(1)先根据非负数的性质求得m=140,n=20,即得∠AOC=140°,∠BOC=20°,从而得到结果; (2)设他们旋转x秒时,使得∠POQ=10°,则∠AOQ=x°,∠BOP=4x°,分局①当射线OP与射线OQ相遇前,②当射线OP与射线OQ相遇后,两种情况,结合旋转的性质分析即可; (3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°,先根据角平分线的性质可得∠COD的度数,即可求得∠BOD的度数,再根据  即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,即可求得结果. 即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,即可求得结果.(1)∵|3m-420|+(2n-40)2=0 ∴3m-420=0且2n-40=0 ∴m=140,n=20 ∴∠AOC=140°,∠BOC=20° ∴∠AOB=∠AOC+∠BOC=160°; (2)设他们旋转x秒时,使得∠POQ=10°,则∠AOQ=x°,∠BOP=4x° ①当射线OP与射线OQ相遇前有:∠AOQ+∠POQ+∠BOP+∠POQ =∠AOB=160° 即x+4x+10=160,解得x=30; ②当射线OP与射线OQ相遇后有:∠AOQ+∠POQ+∠BOP-∠POQ =∠AOB=160° 即x+4x-10=160,解得x=34 答:当他们旋转30秒或34秒时,使得∠POQ=10°; (3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t° ∵OD为∠AOC的平分线 ∴∠COD=  ∠AOC=70° ∠AOC=70°∴∠BOD=∠COD+∠BOC=70°+20°=90° ∵  ∴∠COE=  ×90°=40° ×90°=40° ∠DOE=30°,∠BOE=20°+40°=60° 即4t=60,t=15 ∴∠DOE=15x° 即15x=30,x=2. 点评:本题知识点较多,综合性强,难度较大,需要学生熟练掌握旋转的性质. |
据专家权威分析,试题“如图l,已知∠AOC=m°,∠BOC=n°且m、n满足等式|3m-420|+(2n-40)2=0..”主要考查你对 点、线、面、体 等考点的理解。关于这些考点的“档案”如下:
点、线、面、体
考点名称:点、线、面、体
- 点动成线,线动成面,面动成体:
长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体。
包围着体的是面,面有平的面和曲的面两种。
夜晚流星划过天空时留下一道明亮的光线,节日的焰火画出的曲线组成优美的图案,这些都给我们以线的形象,面和面相交的地方形成线。
天上的星星、世界地图上的城市等都给我们以点的形象,线和线相交的地方是点。
几何图形都是由点、线、面、体组成的,点是构成图形的基本元素。 - 常见几何体的三视图:


- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:对于下列说法,正确的是()A.过一点有且只有一条直线与已知直线平行B.过一点有且只有一条直线与已知直线垂直C.测量孙浩的跳远成绩,正确做法的依据是“两点之间,线段最短”D.不-七年级数学
下一篇:已知线段AB=8cm,在直线AB上画线段BC,使BC=3cm,则线段AC=cm.-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |