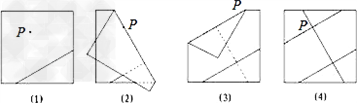
已知直线l及l外一点A,分别按下列要求写出画法,并保留两图痕迹。(1)在图1中,只用圆规在直线l上画出两点B,C,使得点A,B,C是一个等腰三角形的三个顶点;(2)在图2中,只用-九年级数学
由于对尺规作图的限制,使得一些貌似简单的几何作图问题无法解决.最著名的是被称为几何三大问题的三个古希腊古典作图难题:立方倍积问题、三等分任意角问题和化圆为方问题.当时很多有名的希腊数学家,都曾着力于研究这三大问题,虽然借助于其他工具或曲线,这三大难题都可以解决,但由于尺规作图的限制,却一直未能如愿以偿.以后两千年来,无数数学家为之绞尽脑汁,都以失败而告终.直到1637年笛卡尔创立了解析几何,关于尺规作图的可能性问题才有了准则.到了1837年万芝尔首先证明立方倍积问题和三等分任意角问题都属于尺规作图不可能问题.1882年林德曼证明了π是无理数,化圆为方问题不可能用尺规作图解决,这才结束了历时两千年的数学难题公案.
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图,已知∠1=70°,要使AB∥CD,则须具备另一个条件[]A.∠2=70°B.∠2=100°C.∠2=110°D.∠3=110°-九年级数学
下一篇:如图所示,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF。(1)AE与FC会平行吗?说明理由;(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么。-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

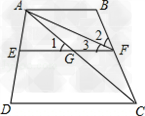

![如图,下列说法中,正确的是[]A.因为∠A+∠D=180°,所以AD∥BCB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AB∥CDD.因为∠A+∠C=180°,所以AB∥CD-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/150/2020-01-07/6a9802b7a026a5297753da5eca5ae992.png)