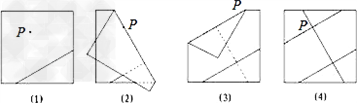
如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB.CD相交于点O,B.D两点立于地面,经测量:AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固-九年级数学
题文
| 如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB.CD相交于点O,B.D两点立于地面,经测量:AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条直线,且EF=32cm. (1)求证:AC∥BD; (2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°); (3)小红的连衣裙穿在衣架后的总长度达到122cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.(参考数据:sin61.9°≈0.882,cos61.9°≈0.471,tan61.9°≈0.553;可使用科学记算器) |
 |
答案
| (1)证明:证法一: ∵AB.CD相交于点O, ∴∠AOC=∠BOD ∵OA=OC, ∴∠OAC=∠OCA=  (180°﹣∠BOD), (180°﹣∠BOD),同理可证:∠OBD=∠ODB=  (180°﹣∠BOD), (180°﹣∠BOD),∴∠OAC=∠OBD ∴AC∥BD, 证法二:AB=CD=136cm,OA=OC=51cm, ∴OB=OD=85cm,又∵  ∴∠AOC=∠BOD∴△AOC∽△BOD, ∴∠OAC=∠OBD∴AC∥  BD; BD;(2)解:在△OEF中,OE=OF=34cm,EF=32cm; 作OM⊥EF于点M,则EM=16cm; ∴cos∠OEF=  0.471,用科学记算器求得∠OEF=61.9°; 0.471,用科学记算器求得∠OEF=61.9°;(3)解法一:小红的连衣裙会拖落到地面; 在Rt△OEM中,  =30cm, =30cm,过点A作AH⊥BD于点H,同(1)可证:EF∥BD, ∴∠ABH=∠OEM,则Rt△OEM∽Rt△ABH, ∴  所以:小红的连衣裙垂挂在衣架后的总长度122cm>晒衣架的高度AH=120cm. 解法二:小红的连衣裙会拖落到地面; 同(1)可证:EF∥BD,∴∠ABD=∠OEF=61.9°; 过点A作AH⊥BD于点H,在Rt△ABH中  , ,AH=AB×sin∠ABD=136×sin61.9°=136×0.882≈120.0cm 分所以:小红的连衣裙垂挂在衣架后的总长度122cm>晒衣架的高度AH=120cm. |
 |
据专家权威分析,试题“如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图..”主要考查你对 平行线的判定,相似三角形的性质 等考点的理解。关于这些考点的“档案”如下:
平行线的判定相似三角形的性质
考点名称:平行线的判定
- 平行线的概念:
在同一个平面内,不相交的两条直线叫做平行线。平行用符号“∥,如“AB∥CD”,读作“AB平行于CD”。
注意:
①平行线是无限延伸的,无论怎样延伸也不相交。
②当遇到线段、射线平行时,指的是线段、射线所在的直线平行。 平行线的判定平行线的判定公理:
(1)两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简称:同位角相等,两直线平行。
(2)两条直线被第三条直线所截,如果内错角相等,那么两直线平行。简称:内错角相等,两直线平行。
(3)两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。简称:同旁内角互补,两直线平行。
还有下面的判定方法:
(1)平行于同一条直线的两直线平行。
(2)垂直于同一条直线的两直线平行。
(3)平行线的定义。判定方法的逆应用:
在同一平面内,两直线不相交,即平行。
两条直线平行于一条直线,则三条不重合的直线互相平行。
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
6a⊥c,b⊥c则a∥b。
考点名称:相似三角形的性质
相似三角形性质定理:
(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
(6)相似三角形内切圆、外接圆直径比和周长比都和相似比相同,内切圆、外接圆面积比是相似比的平方
(7)若a/b =b/c,即b2=ac,b叫做a,c的比例中项
(8)c/d=a/b 等同于ad=bc.
(9)不必是在同一平面内的三角形里
①相似三角形对应角相等,对应边成比例.
②相似三角形对应高的比,对应中线的比和对应角平分线的比都等于相似比.
③相似三角形周长的比等于相似比定理推论:
推论一:顶角或底角相等的两个等腰三角形相似。
推论二:腰和底对应成比例的两个等腰三角形相似。
推论三:有一个锐角相等的两个直角三角形相似。
推论四:直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。
推论五:如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
推论六:如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

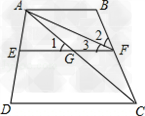

![如图,下列说法中,正确的是[]A.因为∠A+∠D=180°,所以AD∥BCB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AB∥CDD.因为∠A+∠C=180°,所以AB∥CD-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/150/2020-01-07/6a9802b7a026a5297753da5eca5ae992.png)