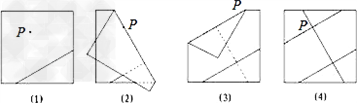
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,OC交AB于E.(1)求∠D的度数;(2)求证:AC2=AD?CE;(3)求BCCD的值.-数学
题文
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D, OC交AB于E. OC交AB于E.(1)求∠D的度数; (2)求证:AC2=AD?CE; (3)求
|
答案
| (1)如图,连接OB(1分) ∵⊙O的内接△ABC中,∠BAC=45°, ∴∠BOC=2∠BAC=90° ∵OB=OC, ∴∠OBC=∠OCB=45° ∵AD∥OC, ∴∠D=∠OCB=45°(2分) (2)证明:∵∠BAC=45°,∠D=45°, ∴∠BAC=∠D(3分) ∵AD∥OC, ∴∠ACE=∠DAC(4分) ∴△ACE∽△DAC ∴
∴AC2=AD?CE(5分)  (3)方法一:如图,延长BO交DA的延长线于F,连接OA ∵AD∥OC, ∴∠F=∠BOC=90° ∵∠ABC=15°, ∴∠OBA=∠OBC-∠ABC=30° ∵OA=OB, ∴∠FOA=∠OBA+∠OAB=60°,∠OAF=30°、 ∴OF=
∵AD∥OC, ∴△BOC∽△BFD ∴
∴
方法二:作OM⊥BA于M,设⊙O的半径为r,可得BM=
ME=OM?tan30°=
|


![如图,下列说法中,正确的是[]A.因为∠A+∠D=180°,所以AD∥BCB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AB∥CDD.因为∠A+∠C=180°,所以AB∥CD-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/150/2020-01-07/6a9802b7a026a5297753da5eca5ae992.png)