题文

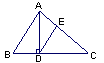
如图，AB∥CD，∠BAC与∠DCA的平分线相交于点G，GE⊥AC于点E，F为AC上的一点，且FA=FG=FC，GH⊥CD于H．下列说法：①AG⊥CG；②∠BAG=∠CGE；③S△AFG=S△CFG；④若∠EGH：∠ECH=2：7，则∠EGF=50度．其中正确的有（　　） A．①②③④ B．②③④ C．①③④ D．①②④

题型：单选题  难度：中档

答案

①中，根据两条直线平行，同旁内角互补，得∠BAC+∠ACD=180°， 再根据角平分线的概念，得∠GAC+∠GCA= 1 2 ∠BAC+ 1 2 ∠ACD= 1 2 ×180°=90°， 再根据三角形的内角和是180°，得AG⊥CG； ②中，根据等角的余角相等，得∠CGE=∠GAC，故∠BAG=∠CGE； ③中，根据三角形的面积公式， ∵AF=CF，∴S△AFG=S△CFG； ④中，根据题意，得：在四边形GECH中，∠EGH+∠ECH=180度． 又∠EGH：∠ECH=2：7，则∠EGH=180°× 2 9 =40°，∠ECH=180°× 7 9 =140度． ∵CG平分∠ECH，∴∠FCG= 1 2 ∠ECH=70°， 根据直角三角形的两个锐角互余，得∠EGC=20°． ∵FG=FC， ∴∠FGC=∠FCG=70°， ∴∠EGF=50°． 故上述四个都是正确的． 故选A．

据专家权威分析，试题“如图，AB∥CD，∠BAC与∠DCA的平分线相交于点G，GE⊥AC于点E，F为AC上..”主要考查你对  平行线的性质，平行线的公理，三角形的周长和面积，多边形的内角和和外角和  等考点的理解。关于这些考点的“档案”如下：

平行线的性质，平行线的公理三角形的周长和面积多边形的内角和和外角和

考点名称：平行线的性质，平行线的公理

• 平行公理：过直线外一点有且只有一条直线与已知直线平行。
  推论（平行线的传递性）：平行同一直线的两直线平行。
  ∵a∥c，c ∥b
  ∴a∥b。

  平行线的性质：
  1. 两条平行被第三条直线所截，同位角相等。
  简单说成：两直线平行，同位角相等。
  2. 两条平行线被第三条直线所截，内错角相等。
  简单说成：两直线平行，内错角相等。
  3 . 两条平行线被第三条直线所截，同旁内角互补。
  简单说成：两直线平行，同旁内角互补。

• 平行线的性质公理注意：
  ①注意条件“经过直线外一点”，若经过直线上一点作已知直线的平行线，就与已知直线重合了；
  ②平行公理体现了平行线的存在性和唯一性；
  ③平行公理的推论体现了平行线的传递性。
  ④在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论。这是平行线特有的性质。不要一提同位角或内错角就认为他们相等，一提同旁内角就认为互补，若没有两直线平行的条件，他们是不成立的。
  

考点名称：三角形的周长和面积

• 三角形的概念：
  由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
  
  构成三角形的元素：
  边：组成三角形的线段叫做三角形的边；
  顶点：相邻两边的公共端点叫做三角形的顶点；
  内角：相邻两边所组成的角叫做三角形的内角，简称三角形的角。
  
  三角形有下面三个特性：
  （1）三角形有三条线段；
  （2）三条线段不在同一直线上；
  （3）首尾顺次相接。
  
  三角形的表示：
  用符号“△，顶点是A、B、C的三角形记作“△ABC”，读作ABC”。

• 三角形的分类：
  （1）三角形按边的关系分类如下：
  ；
  （2）三角形按角的关系分类如下：
  
  把边和角联系在一起，我们又有一种特殊的三角形：等腰直角三角形。它是两条直角边相等的直角三角形。

• 三角形的周长和面积：
  三角形的周长等于三角形三边之和。
  三角形面积=（底×高）÷2。

考点名称：多边形的内角和和外角和

• 在平面内，由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。
  对角线：在多边形中，连接不相邻的两个顶点的线段叫做多边形的对角线。
  外角：多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
  如图示:
  
  多边形的内角和：
  n边形的内角和等于（n-2）·180°。(多边形内角和定理)
  多边形的外角和：
  在多边形的每个顶点处取多边形的一个外角，它们的和叫做多边形的外角和。
  多边形的外角和等于360°。（与边数无关）