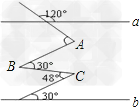
如图1,直线AC∥BD,直线AC、BD及直线AB把平面分成(1)、(2)、(3)、(4)、(5)、(6)六个部分.点P是其中的一个动点,连接PA、PB,观察∠APB、∠PAC、∠PBD三个角.规定:直线AC、BD、A-数学
题文
| 如图1,直线AC∥BD,直线AC、BD及直线AB把平面分成(1)、(2)、(3)、(4)、(5)、(6)六个部分.点P是其中的一个动点,连接PA、PB,观察∠APB、∠PAC、∠PBD三个角.规定:直线AC、BD、AB上的各点不属于(1)、(2)、(3)、(4)、(5)、(6)六个部分中的任何一个部分. 当动点P落在第(1)部分时,可得:∠APB=∠PAC+∠PBD,请阅读下面的解答过程,并在相应的括号内填注理由 过点P作EF∥AC,如图2 因为AC∥BD(已知),EF∥AC(所作), 所以EF∥BD______. 所以∠BPE=∠PBD______. 同理∠APE=∠PAC. 因此∠APE+∠BPE=∠PAC+∠PBD______, 即∠APB=∠PAC+∠PBD. (1)当动点P落在第(2)部分时,∠APB、∠PAC、∠PBD之间的关系是怎样的?请直接写出∠APB、∠PAC、∠PBD之间满足的关系式,不必说明理由. (2)当动点P在第(3)部分时,∠APB、∠PAC、∠PBD之间的关系是怎样的?请直接写出相应的结论. (3)当动点P在第(4)部分时,∠APB、∠PAC、∠PBD之间的关系是怎样的?请直接写出相应的结论.  |