说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.因为AB∥CD(已知),所以∠AGF+______=180°(______),因为GH平分∠AGF,MN平分∠CMG(______),所以∠1=12∠-数学
题文
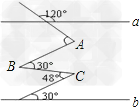
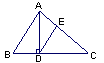
| 说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由. 因为AB∥CD(已知), 所以∠AGF+______=180°(______ ), 因为GH平分∠AGF,MN平分∠CMG(______ ), 所以∠1=
得∠1+∠2=
所以GH⊥MN(______). 根据已知条件和所得结论请总结出一个规律:______.  |