如图,∠1=∠2,DE⊥BC,AB⊥BC.求证:∠A=∠3.证明:因为DE⊥BC,AB⊥BC(已知)因为∠DEC=∠ABC=90°(______)所以DE∥AB(______)所以∠2=______(______)∠1=______(______)又∠1=∠2(已知),所-数学
题文
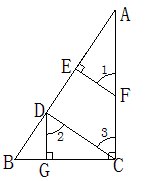
| 如图,∠1=∠2,DE⊥BC,AB⊥BC. 求证:∠A=∠3. 证明:因为DE⊥BC,AB⊥BC(已知) 因为∠DEC=∠ABC=90°(______) 所以DE∥AB(______) 所以∠2=______(______) ∠1=______(______) 又∠1=∠2(已知),所以∠A=∠3(等量代换).  |

![如图,∠AOB=∠COD=90°,则∠AOB+∠COD[]A.大于180°B.小于180°C.等于180°D.以上答案都可能成立-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/153/2020-01-06/7f91ad736b95da9cc5086e32cb386c64.png)