对非负实数x“四舍五入”到个位的值记为<x>即:当n为非负整数时,如果,则<x>=n,如:<0>=<0.48>=0,<0.64>=<1.493>=1,&l-九年级数学
题文
| 对非负实数x“四舍五入”到个位的值记为 即:当n为非负整数时,如果  ,则<x> ,则<x>如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,… 试解决下列问题: (1)填空:①<π>=____(π为圆周率); ②如果<2x-1>=3,则实数x的取值范围为____; (2)①当  ;m为非负整数时,求证:<x+m>=m+<x>; ;m为非负整数时,求证:<x+m>=m+<x>;②举例说明  不恒成立; 不恒成立;(3)求满足  的所有非负实数x的值; 的所有非负实数x的值;(4)设n为常数,且为正整数,函数y=x2-x+  的自变量x在n≤x≤n+1范围内取值时,函数值y为整数的个数记为a;满足 的自变量x在n≤x≤n+1范围内取值时,函数值y为整数的个数记为a;满足 的所有整数k的个数记为b,求证:a=b=2n。 的所有整数k的个数记为b,求证:a=b=2n。 |
答案
解:(1)①3;②  ; ;(2)①证明: 设<x> 则n-  ≤x<n+ ≤x<n+ ,n为非负整数; ,n为非负整数;又(n+m)-  ≤x+m<(n+m)+ ≤x+m<(n+m)+ ,且m+n为非负整数, ,且m+n为非负整数,②举反例:<0.6>+<0.7>=1+1=2, 而<0.6+0.7>=<1.3>=1, ∴<0.6>+<0.7>≠<0.6+0.7>, ∴<x>  的图象,如图 的图象,如图 y=<x>  图象交于点(0,0)、 图象交于点(0,0)、 、 、 , ,∴x=0,  ; ;(4)∵函数y=x2-x+  =(x- =(x- )2,n为整数, )2,n为整数,当n≤x<n+1时,y随x的增大而增大, ∴(n-  )2≤y<(n+1- )2≤y<(n+1- )2, )2,即(n-  )2≤y<(n+ )2≤y<(n+ )2,① )2,①∴n2-n+  ≤y<n2+n+ ≤y<n2+n+ , ,∵y为整数, ∴y=n2-n+1,n2-n+2,n2-n+3,…,n2-n+2n,共2n个y, ∴a=2n②, 则  ,③ ,③比较①,②,③得:a=b=2n。 |
据专家权威分析,试题“对非负实数x“四舍五入”到个位的值记为<x>即:当n为非负整..”主要考查你对 科学记数法和有效数字 等考点的理解。关于这些考点的“档案”如下:
科学记数法和有效数字
考点名称:科学记数法和有效数字
- 定义:
把一个大于10的数表示成a×10n的形式(其中a是整数数位只有一位的数,n是正整数),这种计数法叫做科学记数法。
有效数字:
从一个数的左边非0数字其,到末尾数字止,所有数字都是这个数的有效数字。 - 科学记数法的特点:
(1)简单:对于数目很大的数用科学记数法的形式表示起来又科学、又简单。
(2)科学记数法的形式是由两个数的乘积组成的,其中一个因数为a(1≤a<10,a∈N*),另一个因数为10n(n是比原来数A的整数部分少1的正整数)。
(3)用科学记数法表示数时,不改变数的符号,只是改变数的书写形式而已。 速写法:
对于10的指数大于0的情形,数出“除了第一位以外的数位”的个数,即代表0的个数。
如1800000000000,除最高位1外尚有12位,故科学记数法写作1.8×1012或1.8E12。
10的指数小于0的情形,数出“非有效零的总数(第一个非零数字前的所有零的总数)”
如0.00934593,第一位非零数字(有效数字)9前面有3个零,科学记数法写作9.34593×10-3或9.34593E-3。即第一位非零数字前的0的个数为n,就为10-n(n≥0)
科学计数法的基本运算:
数字很大的数,一般我们用科学记数法表示,
例如6230000000000,我们可以用6.23×1012表示,
而它含义从直面上看是将数字6.23中6后面的小数点向右移去12位。
若将6.23×1012写成6.23E12,
即代表将数字6.23中6后面的 小数点向右移去12位,在记数中如
1. 3×104+4×104=7×104可以写成3E4+4E4=7E4
即 aEc+bEc=(a+b)Ec
2. 4×104-7×104=-3×104可以写成4E4-7E4=-3E4
即 aEc-bEc=(a-b)Ec
3. 3000000×600000=1800000000000
3e6×6e5=1.8e12
即 aEM×bEN=abE(M+N)
4. -60000÷3000=-20
-6E4÷3E3=-2E1
即 aEM÷bEN=a/bE(M-N)
5.有关的一些推导
(aEc)2=(aEc)(aEc)=a2E2c
(aEc)3=(aEc)(aEc)(aEc)=a3E3c
(aEc)n=anEnc
a×10lgb=ab
aElgb=ab
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

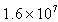
![信息时代,“网上冲浪”已成为人们生活中不可缺少的一部分,预计到2010年,我国网民数有望突破2亿人,下面关于“2亿”的说法错误的是[]A.这是一个精确数B.这是一个近似数C.2亿-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/17/2019-02-21/87de750e1a3b8958eab75ed1b716c87b.gif)
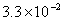
![我们身处在自然环境中,一年接受的宇宙射线及其它天然辐射照射量约为3100微西弗(1西弗等于1000毫西弗,1毫西弗等于1000微西弗),用科学记数法可表示为[]A.西弗B.西弗C.西-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/17/2019-02-21/94cd328342379072e4a237d291e91fbe.gif)
![我国西部地区约占我国国土面积的,我国国土面积约960万平方公里.若用科学记数法表示,则我国西部地区的面积为[]A.6.4×106平方公里B.6.4×107平方公里C.640×104平方公里D.64-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/17/2019-02-22/a84710d7f989a306a95a00387561d7f6.png)
