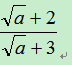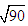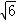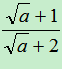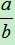任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[3]=1,现对72进行如下操作:72第一次[72]=8第二次[8]=2第三次[2]=1,这样对72只需进行3次操作后变为1,类似地:(1)对81只-数学
题文
| 任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[3]=1,现对72进行如下操作: 72
(1)对81只需进行______次操作后变为1; (2)只需进行3次操作后变为1的所有正整数中,最大的是______. |
答案
(1)∵[
∴对81只需进行3次操作后变为1, 故答案为:3. (2)最大的正整数是255, 理由是:∵[
∴对255只需进行3次操作后变为1, ∵[
∴对256只需进行4次操作后变为1, ∴只需进行3次操作后变为1的所有正整数中,最大的是255, 故答案为:255. |
据专家权威分析,试题“任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[3]=1,现对..”主要考查你对 估算无理数的大小 等考点的理解。关于这些考点的“档案”如下:
估算无理数的大小
考点名称:估算无理数的大小
- 在一些题目中我们常常需要估算无理数的取值范围,要想准确地估算出无理数的取值范围需要记住一些常用数的平方。一般情况下从1到达20整数的平方都应牢记。
例:估算 的取值范围。
的取值范围。
解:因为1<3<4,所以 <
< <
< ,
,
即:1< <2如果想估算的更精确一些,
<2如果想估算的更精确一些,
比如说想精确到0.1.可以这样考虑:因为17的平方是289,18的平方是324,所以1.7的平方是2.89,1.8的平方是3.24.
因为2.89<3<3.24,
所以 <
< <
< ,
,
所以1.7< <1.8。
<1.8。
如果需要估算的数比较大,可以找几个比较接近的数值验证一下。 比较无理数大小的几种方法:
比较无理数大小的方法很多,在解题时,要根据所给无理数的特点,选择合适的比较方法。
一、直接法
直接利用数的大小来进行比较。
①、同是正数:
例:<?xml:namespace prefix = "v" ns = "urn:schemas-microsoft-com:vml" />
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:若13-1的整数部分是a,313的小数部分是b;①则a=______,②则(a+b)6=______.-数学
下一篇:如图,数轴上点P表示的数可能是()A.-10B.7C.-7D.-3.3-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |