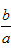设抛物线y=x2+(2a+1)x+2a+54的图象与x轴只有一个交点.(1)求a的值;(2)求a18+323a-6的值.-数学
题文
设抛物线y=x2+(2a+1)x+2a+
(1)求a的值; (2)求a18+323a-6的值. |
答案
(1)∵抛物线y=x2+(2a+1)x+2a+
∴△=(2a+1)2-4×1×(2a+
解得:a=
(2)∵a=
∴a是方程x2-x-1=0的根, ∴a2-a-1=0, ∵a≠0, ∴a-
a2+
=(a-
=3, a4+
=(a2+
=7, a8+
=(a4+
=47, a12+
=(a4+
=7×(47-1) =322, a18+323a-6 =(a18+
=a6(a12+
=322a6+
=322(a6+
a6+
=(a2+
=3×(7-1) =18. ∴322(a6+
|


![如图,要使输出Y大于100,则输入的最小正整数X的值是[]A.22B.21C.19D.18-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/25/2019-02-27/3cf3eaedab08653ff4d9fe2d4401149d.gif)
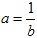
![已知a、b互为相反数,c、d互为倒数,x=16,则式子的值为[]A.2B.4C.8D.﹣8-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/25/2019-02-27/b13fb8cd04b0467f4301a11c2bbfc187.png)