已知式子M:3x2-4x+7,式子N:4x2-4x+7,那么M、N两式值的大小关系是[]A.M>NB.M<NC.M=ND.M≤N-七年级数学
题文
| 已知式子M:3x2-4x+7,式子N:4x2-4x+7,那么M、N两式值的大小关系是( ) |
|
A.M>N B.M<N C.M=N D.M≤N |
答案
| D |
据专家权威分析,试题“已知式子M:3x2-4x+7,式子N:4x2-4x+7,那么M、N两式值的大小关系..”主要考查你对 不等式的比较大小 等考点的理解。关于这些考点的“档案”如下:
不等式的比较大小
考点名称:不等式的比较大小
- 主要是运用不等式的基本性质及均值不等式进行比较大小。
方法:
①求差比较法的基本步骤是:“作差——变形——断号”。
其中,作差是依据,变形是手段,判断符号才是目的。变形的目的全在于判断差的符号,而不必考虑差值是多少:
变形的方法一般有配方法、通分的方法和因式分解的方法等,为此,有时把差变形为一个常数,或者变形为一个常数与一个或几个数的平方和的形式。或者变形为一个分式,或者变形为几个因式的积的形式等。总之,能够判断出差的符号是正或负即可。②作商比较法的基本步骤是:“作商——变形——判断商式与1的大小关系”,需要注意的是,作商比较法一般用于不等号两侧的式子同号的不等式的证明。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:若-1≤a<0,则a、-a、三者的大小关系满足[]A.a≥≥-aB.≤a<-aC.≥a>-aD.≤a≤-a-七年级数学
下一篇:一家三人准备参加旅游团外出旅游,甲旅行社告之:“父母买全票,女儿按半票优惠”,乙旅行社告之:“家庭旅游可以按团体票计价,每人均按全价的收取,”如果这两家旅行社每人的原票-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![己知a,b两数在数轴上对应的点如图所示,下列结论正确的是[]A.a>bB.ab<0C.b﹣a>0D.a+b>0-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/55/2019-03-19/c522844f070808ac5d8e936b647f03ce.png)
![已知a、b在数轴上的位置如图所示,那么下面结论正确的是[]A.a-b<0B.a+b>0C.ab<0D.>0-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/55/2019-03-19/48d10a4931fe81d161cd890213767c45.gif)
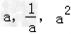
![有理数a、b在数轴上的位置如图示,则[]A.a+b<0B.a+b>0C.a-b=0D.a-b>0-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/55/2019-03-19/ab874fc05d24f20451bbbbdbfb374a4e.gif)
![若0<x<1,则x,,x2的大小关系是[]A.<x<x2B.x<<x2C.x2<x<D.<x2<x-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/55/2019-03-19/24bb60ff171815f1ed37a0fa9ab0dd41.gif)
