已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm。①试写出长方形的周长y与x之间的关系式;②求当x长为10cm,15cm时的周长;③求当周长分别为20cm,30cm时的x值。-七年级数学
题文
| 已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm。 ①试写出长方形的周长y与x之间的关系式; ②求当x长为10cm,15cm时的周长; ③求当周长分别为20cm,30cm时的x值。 |
答案
| 解:①y=2x+8;②28cm,38cm;③6;11。 |
据专家权威分析,试题“已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm。..”主要考查你对 变量及函数 等考点的理解。关于这些考点的“档案”如下:
变量及函数
考点名称:变量及函数
函数:一般地,在一个变化过程中,如果有两个自变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
变量:
在一个变化过程中,我们称数值发生变化的量为变量。(数学中,常常为x,而y则随x值的变化而变化),有些数值是不随变量而改变的,我们称它们为常量。
自变量:函数一个与它量有关联的变量,这一量中的任何一值都能在它量中找到对应的固定值。
因变量(函数):随着自变量的变化而变化,且自变量取唯一值时,因变量(函数)有且只有唯一值与其相对应。- 变量的关系:
在具体情境中,感受两个变量之间的关系,就是一个变量随着另一个变量的变化情况,例如随着一个变量的变化,有的变量是呈匀速变化的,有的变量是呈不匀速变化的;
进而发现实际情景中的变量及其相互关系,并确定其中的自变量和因变量,会用运动变化的基本观点观察事物。也就是说,在两个有相依关系的变量中,其中一个是自变量,另一个是因变量;
自变量和因变量之间的变化关系可以用表格来刻画,也可以用图象来描述,并能对未来的趋势加以预测。 - 函数自变量的取值范围的确定:
使函数有意义的自变量的取值的全体,叫做函数自变量的取值范围.
自变量的取值范围的确定方法:
首先要考虑自变量的取值必须使解析式有意义,
①当解析式为整式时,自变量的取值范围是全体实数;
②当解析式是分数的形式时,自变量的取值范围是使分母不为零的所有实数;
③当解析式中含有平方根时,自变量的取值范围是使被开方数不小于零的实数;
④当函数解析式表示实际问题时,自变量的取值必须使实际问题有意义。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
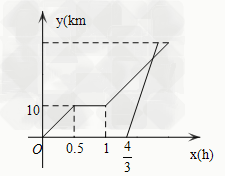
上一篇:小明读七年级,他很想一个人郊外秋游,但妈妈不放心,让他将一天的时间安排做一个详细计划,于是小明绘制了下图交给妈妈,你能根据这幅图想象一下小明的秋游情况吗?-七年级数学
下一篇:洪山县从2000年开始实施退耕还休,每年退耕还休的面积如下表:①上表反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?②从表中可知,随时间的变化,退耕还林面积的变化-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |