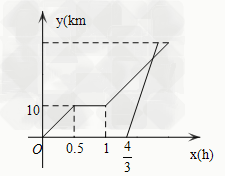
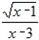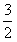弹簧的长度与所挂物体的质量的关系如图所示,由图可知不挂重物时弹簧的长度为[]A.8cmB.9cmC.10cmD.11cm-七年级数学
题文
| 弹簧的长度与所挂物体的质量的关系如图所示,由图可知不挂重物时弹簧的长度为 |
|
|
|
[ ] |
| A.8cm B.9cm C.10cm D.11cm |
答案
| C |
据专家权威分析,试题“弹簧的长度与所挂物体的质量的关系如图所示,由图可知不挂重物时..”主要考查你对 变量及函数 等考点的理解。关于这些考点的“档案”如下:
变量及函数
考点名称:变量及函数
函数:一般地,在一个变化过程中,如果有两个自变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
变量:
在一个变化过程中,我们称数值发生变化的量为变量。(数学中,常常为x,而y则随x值的变化而变化),有些数值是不随变量而改变的,我们称它们为常量。
自变量:函数一个与它量有关联的变量,这一量中的任何一值都能在它量中找到对应的固定值。
因变量(函数):随着自变量的变化而变化,且自变量取唯一值时,因变量(函数)有且只有唯一值与其相对应。- 变量的关系:
在具体情境中,感受两个变量之间的关系,就是一个变量随着另一个变量的变化情况,例如随着一个变量的变化,有的变量是呈匀速变化的,有的变量是呈不匀速变化的;
进而发现实际情景中的变量及其相互关系,并确定其中的自变量和因变量,会用运动变化的基本观点观察事物。也就是说,在两个有相依关系的变量中,其中一个是自变量,另一个是因变量;
自变量和因变量之间的变化关系可以用表格来刻画,也可以用图象来描述,并能对未来的趋势加以预测。 - 函数自变量的取值范围的确定:
使函数有意义的自变量的取值的全体,叫做函数自变量的取值范围.
自变量的取值范围的确定方法:
首先要考虑自变量的取值必须使解析式有意义,
①当解析式为整式时,自变量的取值范围是全体实数;
②当解析式是分数的形式时,自变量的取值范围是使分母不为零的所有实数;
③当解析式中含有平方根时,自变量的取值范围是使被开方数不小于零的实数;
④当函数解析式表示实际问题时,自变量的取值必须使实际问题有意义。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的高度y(cm)与燃烧时间x(小时)的关系用下图中的图象表示,合适的是[]A.B.C.D.-七年级数学
下一篇:声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下:从表中可知音速y随温度x的升高而(),在气温为20℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |