下面共有四种情景:A.一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系);B.从树上开始往下掉的苹果(苹果落地前的高度与下落时间的关系);C.一杯越来越凉的开水(水温与时-数学
题文
| 下面共有四种情景: A.一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系); B.从树上开始往下掉的苹果(苹果落地前的高度与下落时间的关系); C.一杯越来越凉的开水(水温与时间的关系); D.竖直向上抛出的篮球(篮球落地前的速度与时间的关系); 上面各种情景可以近似的用下面哪个图象来表示(横轴表示时间,纵轴表示相应的因变量),A、B、C、D各情景对应的图象依次为:______.  |

![如图,一个蓄水桶,60分钟可将一满桶水放干,其中,水位h(cm)随着放水时间t(分)的变化而变化,放水速度恒定,h与t的函数的大致图像为[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/62/2019-03-23/35420515a8ba0d2c4300b8bae2256249.gif)
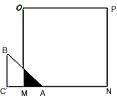
![如图,在矩形中,AB=2,,动点P从点B出发,沿路线作匀速运动,那么△ABP的面积S与点P运动之间的函数图象大致是[]A.B.C.D.-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/62/2019-03-23/09fbc2f932633f83492aebd7276430d5.png)
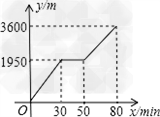
![如图,正方形ABCD的边长为a,动点P从点A出发,沿折线A→B→D→C→A的路径运动,回到点A时运动停止.设点P运动的路程长为长为x,AP长为y,则y关于x的函数图象大致是[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/62/2019-03-23/3727ad4df87fbc5a147244e00f1c8163.png)
