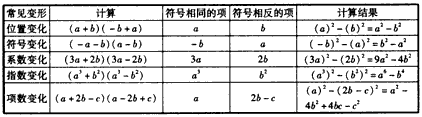
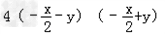观察下列计算:12+1=2-1,13+2=3-2,14+3=4-3,15+4=5-4…从计算结果中找出规律,并利用这一规律计算:(12+1+13+2+14+3+…+12008+2007)(2008+1)=______.-数学
题文
观察下列计算:
|
答案
原式=(
=(
=2008-1 =2007. 故答案为:2007. |
据专家权威分析,试题“观察下列计算:12+1=2-1,13+2=3-2,14+3=4-3,15+4=5-4…从计算结..”主要考查你对 平方差公式,最简二次根式 等考点的理解。关于这些考点的“档案”如下:
平方差公式最简二次根式
考点名称:平方差公式
- 表达式:
(a+b)(a-b)=a2-b2,两个数的和与这两个数差的积,等于这两个数的平方差,这个公式就叫做乘法的平方差公式。 - 特点:
(1)左边是两项式相乘,一项完全相同,另一项互为相反数;
(2)右边是乘方中两项的平方差。
注:
(1)公式中的a和b可以是具体的数也可以是单项式或多项式;
(2)不能直接应用公式的,要善于转化变形,运用公式。 常见错误:
平方差公式中常见错误有:
①学生难于跳出原有的定式思维,如典型错误;(错因:在公式的基础上类推,随意“创造”)
②混淆公式;
③运算结果中符号错误;
④变式应用难以掌握。注意事项:
1、公式的左边是个两项式的积,有一项是完全相同的。
2、右边的结果是乘式中两项的平方差,相同项的平方减去相反项的平方。
3、公式中的a.b 可以是具体的数,也可以是单项式或多项式。
考点名称:最简二次根式
最简二次根式定义:
被开方数中不含字母,并且被开方数中所有因式的幂的指数都小于2,这样的二次根式称为最简二次根式。
有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,则说这两个代数式互为有理化因式。- 最简二次根式同时满足下列三个条件:
(1)被开方数的因数是整数,因式是整式;
(2)被开方数中不含有能开的尽的因式;
(3)被开方数不含分母。 - 最简二次根式判定:
①在二次根式的被开方数中,只要含有分数或小数就不是最简二次根式;
②在二次根式的被开方数中的每一个因式(或因数),如果幂的指数等于或大于2,也不是最简二次根式。
化二次根式为最简二次根式的方法和步骤:
①如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简。
②如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

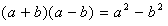
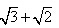
![如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为[]A.(a﹣b)2=a-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/75/2019-04-05/98b29dedad152884a72be7436180e66a.png)