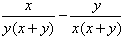题文

计算下列各式： （1） 1 a-b + 1 a+b + 2a a2+b2 + 4a3 a4+b4 ； （2） x2+yz x2+(y-z)x-yz + y2-zx y2+(z+x)y+zx + z2+xy z2-(x-y)z-xy ； （3） x3-1 x3+2x2+2x+1 + x3+1 x3-2x2+2x-1 - 2(x2+1) x2-1 （4） (y-x)(z-x) (x-2y+z)(x+y-2z) + (z-y)(x-y) (x+y-2z)(y+z-2x) + (x-z)(y-z) (y+z-2x)(x-2y+z) ．

题型：解答题  难度：中档

答案

（1） 1 a-b + 1 a+b + 2a a2+b2 + 4a3 a4+b4 = 2a a2-b2 + 2a a2+b2 + 4a3 a4+b4 = 4a3 a4-b4 + 4a3 a4+b4 = 8a7 a8-b8 ； （2） x2+yz x2+(y-z)x-yz + y2-zx y2+(z+x)y+zx + z2+xy z2-(x-y)z-xy = x(x-z)+z(x+y) (x+y)(x-z) + y(x+y)-x(y+z) (x+y)(y+z) + z(y+z)-y(z-x) (z-x)(y+z) = x x+y + z x-z + y y+z - x x+y - z x-z - y y+z =0； （3） x3-1 x3+2x2+2x+1 + x3+1 x3-2x2+2x-1 - 2(x2+1) x2-1 = (x-1)(x2+x+1) (x+1)(x2+x+1) + (x+1)(x2-x+1) (x-1)(x2-x+1) - 2(x2+1) (x+1)(x-1) = x-1 x+1 + x+1 x-1 - 2(x2+1) (x+1)(x-1) =0； （4）设x-y=a，y-z=b，z-x=c，则 (y-x)(z-x) (x-2y+z)(x+y-2z) + (z-y)(x-y) (x+y-2z)(y+z-2x) + (x-z)(y-z) (y+z-2x)(x-2y+z) =- ac (a-b)(b-c) - ab (b-c)(c-a) - cb (c-a)(c-b) =- ac(c-a)+ab(a-b)+bc(b-c) (a-b)(b-c)(c-a) = (a-b)(b-c)(c-a) (a-b)(b-c)(c-a) =1．

据专家权威分析，试题“计算下列各式：（1）1a-b+1a+b+2aa2+b2+4a3a4+b4；（2）x2+yzx2+(y-z)..”主要考查你对  分式的加减  等考点的理解。关于这些考点的“档案”如下：

分式的加减

考点名称：分式的加减

• 分式的加减法则：
  同分母的分式相加减，分母不变，把分子相加减；
  异分母的分式相加减，先通分，变为同分母分式，然后再加减。
  用式子表示为：
  

• 分式的加减要求：
  ①分式的加减运算结果必须是最简分式或整式，运算中要适时地约分；
  ②如果一个分式与一个整式相加减，那么可以把整式看成是分母为1的分式，先通分，再进行加减。