李爷爷从二楼上四楼用了分钟,照这样的速度,他从一楼上到六楼需要多长时间?-六年级数学
题文
李爷爷从二楼上四楼用了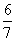 分钟,照这样的速度,他从一楼上到六楼需要多长时间? 分钟,照这样的速度,他从一楼上到六楼需要多长时间? |
答案
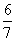 ÷(3-1)×(6-1)= ÷(3-1)×(6-1)= (分) (分) |
据专家权威分析,试题“李爷爷从二楼上四楼用了分钟,照这样的速度,他从一楼上到六楼需..”主要考查你对 分数乘法及应用,植树问题 等考点的理解。关于这些考点的“档案”如下:
分数乘法及应用植树问题
考点名称:分数乘法及应用
分数的乘法:
分数的分子与分子相乘,分母与分母相乘,能约分的要先约分。做第一步时,就要想一个数的分子和另一个分母能不能约分。
分数与整数相乘就是把多个同样的数叠加,如2/3x2,就是指2个2/3相加,2/3x10是指10个2/3相加。
应用:
求一个数的几分之几是多少,用乘法来计算。
“求一个数的几倍是多少”和“求一个数的几分之几是多少”的数量关系是相同的。
一个数乘分数实际也是求这个数的几分之几倍,习惯上把“倍”省去,就说求这个数的几分这几。
特征:
已知条件表示单位“1”的量,单位“1”的几分之几。所求问题:求单位“1”的几分之几。
考点名称:植树问题
植树问题:
把研究植树的棵树、株距与线路总长之间关系的问题称为植树问题。- 植树问题公式:
(1)非封闭线路上的植树问题分为以下三种:
①如果在非封闭线路的两端都要植树,那么:
株数=段数+1=全长÷株距+1;
全长=株距×(株数-1);
株距=全长÷(株数-1)。
②如果在非封闭线路的一端要植树,另一端不要植树,那么:
株数=段数=全长÷株距;
全长=株距×株数;
株距=全长÷株数。
③如果在非封闭线路的两端都不要植树,那么:
株数=段数-1=全长÷株距-1;
全长=株距×(株数+1);
株距=全长÷(株数+1)。
(2)在封闭线路上的植树问题的数量关系如下:
株数=段数=全长÷株距;
全长=株距×株数;
株距=全长÷株数。
解决植树问题首先要分清植树线路是否是封闭的;
其次还要注意题目的具体要求(单侧植树还是两侧植树,两端是否植树等)。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

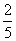
![甲数的等于乙数的,乙数是甲数的3倍。[]-六年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/fenshuchengfajiyingyong/2019-05-23/c6b939e62f7ec2b30def8961a0e156c1.gif)


