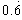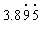对错我知道,对的打“√”,错的打“×”(1)近似数2.0和2完全相同。[](2)含有未知数的等式叫做方程。[](3)n个同样的平行四边形一定能拼成一个较大的平行四边形。[](4)被除数比除数-五年级数学
题文
对错我知道,对的打“√”,错的打“×”
|
答案
| (1)×;(2)√;(3)√;(4)√;(5)√ |
据专家权威分析,试题“对错我知道,对的打“√”,错的打“×”(1)近似数2.0和2完全相同。[]..”主要考查你对 求小数的近似值,平行四边形的认识,和差积商的变化规律,方程的定义,等式的性质 等考点的理解。关于这些考点的“档案”如下:
求小数的近似值平行四边形的认识和差积商的变化规律方程的定义,等式的性质
考点名称:求小数的近似值
- 求近似数:
是根据需要用“四舍五入法”保留一定的小数位数。 - 方法点拨:
求近似数时:保留整数,表示精确到个位;保留一位小数,表示精确到十分位;保留两位小数,表示精确到百分位……
如:豆豆身高0.984米
求:1、保留两位小数: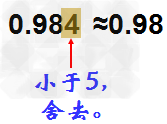
如果保留两位小数,就要第三位数省略。
2、保留一位小数:

如果保留一位小数,就要把第二、三位小数省略。
在表示近似数时,小数末尾的0不能去掉。
3、保留整数部分: ≈1
≈1
省略个位后面的尾数
考点名称:平行四边形的认识
- 认识平行四边形:
(1)
(2)
- 平行四边行的特点:
(1)平行四边形具有不稳定性
(2)平行四边形对边平行且相等
(3)平行四边形对角相等
考点名称:和差积商的变化规律
- 学习目标:
理解并探索运算中蕴含的规律,并应用规律解决问题。 - 和的变化规律
(一)如果一个加数增加一个数,另一个加数不变,那么它们的和也增加同一个数。
(二)如果一个加数减少一个数,另一个加数不变,那么,它们的和也减少同一个数.
(三)如果一个加数增加一个数,另一个加数减少同样的加数,那么,它们的和不变.
(四)如果一个加数增加一个数m,另一个加数增加一个数n,那么,它们的和就增加(m+n).
(五)如果一个加数减少一个数m,另一个加数减少一个数n,那么,它们的和就减少(m+n).
(六)如果一个加数增加一个数m,另一个加数减少一个数n,当m>n时,它们的和就增加(m-n);当m<n时,它们的和就减少(n-m).
差的变化规律
(一)如果被减数增加或减少一个数,减数不变,那么它们的差也增加或减少同一个数.
(二)如果减数增加或减少一个数,被减数不变,那么,它们的差就减少或增加同一个数.
(三)如果被减数和减数同时增加或减少同一个数,那么,它们的差相等.
(四)如果被减数增加一个数m,减数减少一个数n,那么,它们的差就增加(m+n).
(五)如果被减数减少一个数m,减数增加一个数n,那么,它们的差就减少(m+n)
(六)如果被减数增加一个数m,减数增加一个数n,那么,当m>n时,它们的差就增加(m+n);当m<n时,它们的差就减少(n-m).
(七)如果被减数减少一个数m,减数减少一个数n,那么,当m>n时,它们的差要减少(m-n);当m<n时,它们的差要增加(n-m).
积的变化规律
(一)如果一个因数扩大m倍,另一个因数不变,那么,它们的积也扩大m倍.
(二)如果一个因数缩小m倍,另一个因数不变,那么,它们的积也缩小m倍.
(三)如果一个因数扩大m倍,另一个因数缩小相同的倍数,那么它们的积不变.
(四)如果一个因数扩大m倍,另一个因数扩大n倍,那么,它们的积扩大(m×n)倍.
(五)如果一个因数缩小m倍,另一个因数缩小n倍,那么,它们的积就缩小(m×n)倍.
(六)如果一个因数扩大m倍,另一个因数缩小n倍,那么,当m>n时它们的积扩大(m÷n)倍,当m<n时,它们的积就缩小(n÷m)倍.
商的变化规律
(一)如果被除数和除数同时扩大或缩小相同的倍数,那么,它们的商不变.
(二)如果被除数扩大(或缩小)m倍,除数不变,那么,它们的商就扩大(或缩小)m倍.
(三)如果除数扩大或缩小m倍,被除数不变,那么,它们的商反而缩小或扩大m倍.
(四)如果被除数扩大m倍,除数缩小n倍,那么,它们的商就扩大(m×n)倍.
(五)如果被除数缩小m倍,除数扩大n倍,那么,它们的商就缩小(m×n)倍.
(六)如果被除数扩大m倍,除数扩大n倍,当m>n时,它们的商就扩大(m÷n)倍,当m<n时,它们的商就缩小(n÷m)倍.
(七)如果被除数缩小m倍,除数缩小n倍,当m>n时,它们的商就缩小(m÷n)倍,当m<n时,它们的商就扩大(n÷m)倍.
考点名称:方程的定义,等式的性质
- 等式:
含有等号的式子叫做等式(数学术语)。形式:把相等的两个数(或字母表示的数)用“=”连接起来。
方程:
含有未知数的等式叫做方程。即:
1.方程中一定有一个或一个以上含有未知数的代数式;
2.方程式是等式,但等式不一定是方程。 等式基本性质:
性质1
等式两边同时加上(或减去)同一个整式,等式的值不变。
若a=b
那么a+c=b+c
性质2
等式两边同时乘或除以同一个不为0的整式,等式的值不变。
若a=b
那么有a·c=b·c
或a÷c=b÷c (c≠0)
性质3
等式具有传递性。
若a1=a2,a2=a3,a3=a4,……an=an,那么a1=a2=a3=a4=……=an
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |