题文

“月球上有水吗？”根据对某校七年级学生的调查，结果认为“有水”“没有水”“不知道”的人数比为6：3：1，则制成扇形统计图中“有水”的那部分扇形所对应的百分比为______，“没有水”的那部分对应的百分比为______．

题型：填空题  难度：中档

答案

“有水”“没有水”“不知道”的人数比为6：3：1，不知道的人数看成1份，那么认为有水的人数就占6份，认为没有水的人数就占3份， 总人数就是6+3+1=10份； 6÷10=60%； 3÷10=30%； 答：“有水”的那部分扇形所对应的百分比为60%，“没有水”的那部分对应的百分比为30%． 故答案为：60%，30%．

据专家权威分析，试题““月球上有水吗？”根据对某校七年级学生的调查，结果认为“有水”“没..”主要考查你对  扇形统计图，古典概型的定义及计算  等考点的理解。关于这些考点的“档案”如下：

扇形统计图古典概型的定义及计算

考点名称：扇形统计图

• 扇形统计图：
  用整个圆的面积表示总数，用扇形面积表示各部分占总数的百分数。可以清楚地表示出各部分与总数、部分与部分之间的数量关系。

• 扇形统计图特点:
  通过扇形的大小来反映各个部分占总体的百分之几。
  扇形统计图可以更清楚的了解各部分数量同总数之间的关系。
  扇形统计图可以让一些杂乱无章的数据变得清晰透彻，使人看上去一目了然，利于计算各种数据，变得更加方便，快捷！

• 扇形统计图作用:
  能清楚地了解各部分数与总数之间的关系与比例。（比例：表示两个比相等的式子叫做比例的基本性质）
  扇形面积与其对应的圆心角的关系是：
  扇形面积越大，圆心角的度数越大。
  扇形面积越小，圆心角的度数越小。
  扇形所对圆心角的度数与百分比的关系是：圆心角的度数=百分比×360度
  扇形统计图还可以画成圆柱形的。

  制扇形统计图的步骤：
  （1）先算出各部分数量占总数量的百分之几；
  （2）再算出表示各部分数量的扇形的圆心角度数；
  （3）取适当的半径画一个圆，并按照上面算出的圆心角的度数，在圆里画出各个扇形；
  （4）在每个扇形中标明所表示的各部分数量名称和所占的百分数，并用不同的颜色或条纹把各扇形区别开。

考点名称：古典概型的定义及计算

• 基本事件的定义：

  一次试验连同其中可能出现的每一个结果称为一个基本事件。

  等可能基本事件：

  若在一次试验中，每个基本事件发生的可能性都相同，则称这些基本事件为等可能基本事件。

  古典概型：

  如果一个随机试验满足：（1）试验中所有可能出现的基本事件只有有限个；
  （2）每个基本事件的发生都是等可能的；
  那么，我们称这个随机试验的概率模型为古典概型．

  古典概型的概率：

  如果一次试验的等可能事件有n个，那么，每个等可能基本事件发生的概率都是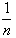；如果某个事件A包含了其中m个等可能基本事件，那么事件A发生的概率为
  。
  

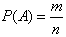• 古典概型解题步骤：

  （1）阅读题目，搜集信息；
  （2）判断是否是等可能事件，并用字母表示事件；
  （3）求出基本事件总数n和事件A所包含的结果数m；
  （4）用公式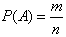求出概率并下结论。

  求古典概型的概率的关键：

  求古典概型的概率的关键是如何确定基本事件总数及事件A包含的基本事件的个数。