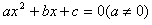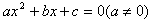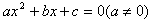题文

阅读材料：如果一元二次方程ax2+bx+c=0（a≠0）的两个实数根分别是x1、x2，那么x1+x2=- b a ，x1?x2= c a ．借助该材料完成下列各题： （1）若x1、x2是方程x2-4x+ 5 =0的两个实数根，x1+x2=______；x1?x2=______． （2）若x1、x2是方程2x2+6x-3=0的两个实数根， 1 x1 + 1 x2 =______； x 21 + x 22 =______． （3）若x1、x2是关于x的方程x2-（m-3）x+m+8=0的两个实数根，且 x 21 + x 22 =13，求m的值．

题型：解答题  难度：中档

答案

（1）∵x1、x2是方程x2-4x+ 5 =0的两个实数根， ∴x1+x2=- -4 1 =4，x1?x2= 5 1 = 5 ； 故答案是：4， 5 ； （2）∵x1、x2是方程2x2+6x-3=0的两个实数根， ∴x1+x2= 6 2 =3，x1?x2= -3 2 =- 3 2 ， ∴ 1 x1 + 1 x2 = x1+x2 x1?x2 = 3 - 3 2 =-2， x 21 + x 22 =（x1+x2）2-2x1?x2=32-2×（- 3 2 ）=12． 故答案是：-2，12； （3）∵关于x的方程x2-（m-3）x+m+8=0有两个实数根， ∴△=（m-3）2-4（m+8）≥0，即m≥5+4 3 ，或m≤5-4 3 ∵x1、x2是关于x的方程x2-（m-3）x+m+8=0的两个实数根， ∴x1+x2=m-3，x1?x2=m+8， ∴ x 21 + x 22 =（x1+x2）2-2x1?x2=13，即（m-3）2-2（m+8）=13， 解得，m=-2或m=10． 即m的值是-2或10．

据专家权威分析，试题“阅读材料：如果一元二次方程ax2+bx+c=0（a≠0）的两个实数根分别是x1..”主要考查你对  一元二次方程根与系数的关系  等考点的理解。关于这些考点的“档案”如下：

一元二次方程根与系数的关系

考点名称：一元二次方程根与系数的关系

• 一元二次方程根与系数的关系：
  如果方程 的两个实数根是那么，。
  也就是说，对于任何一个有实数根的一元二次方程，两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商。

• 一元二次方程根与系数关系的推论：
  1.如果方程x²+px+q=0的两个根是x_1、x_2，那么x₁₊x_2^=-p _^， x_1`x₂₌q
  2.以两个数x₁、x₂为根的一元二次方程（二次项系数为1）是x₂-(x₁+x₂)x+x₁x_2⁼0
  提示：
  ①运用根与系数的关系和运用根的判别式一样，都必须先把方程化为一般形式，以便正确确定a、b、c的值。
  ②有推论1可知，对于二次项系数为1的一元二次方程，他的两根之和等于一次项系数的相反数，两根之积等于常数项。
  ③推论2可以看作推论1的逆定理，利用推论2可以直接求出以两个数x_1、x₂为根的一元二次方程（二次项系数是1）是x₂-(x₁+x₂)x+x₁x_2⁼0