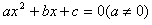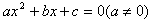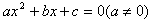已知一元二次方程x2-x+1-m=0的两个实根α,β满足|α|+|β|≤5,则实数m的取值范围是______.-数学
题文
| 已知一元二次方程x2-x+1-m=0的两个实根α,β满足|α|+|β|≤5,则实数m的取值范围是______. |
答案
| ∵一元二次方程x2-x+1-m=0的两个实根, ∴△=1-4(1-m)≥0, ∴m≥
∵一元二次方程x2-x+1-m=0的两个实根α,β满足|α|+|β|≤5, 而α+β=1, αβ=1-m, ∴(|α|+|β|)2≤25, α2+2|αβ|+β2≤25, (α+β)2-2αβ+2|αβ|≤25, ∴1-2(1-m)+2|1-m|≤25, 当m-1≤0即m≤1时,不等式永远成立; 当m>1时,m≤7, ∴
|
据专家权威分析,试题“已知一元二次方程x2-x+1-m=0的两个实根α,β满足|α|+|β|≤5,则实数..”主要考查你对 一元二次方程根与系数的关系 等考点的理解。关于这些考点的“档案”如下:
一元二次方程根与系数的关系
考点名称:一元二次方程根与系数的关系
- 一元二次方程根与系数的关系:
如果方程 的两个实数根是
的两个实数根是 那么
那么 ,
, 。
。
也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商。 一元二次方程根与系数关系的推论:
1.如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p , x1`x2=q
2.以两个数x1、x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)x+x1x2=0
提示:
①运用根与系数的关系和运用根的判别式一样,都必须先把方程化为一般形式,以便正确确定a、b、c的值。
②有推论1可知,对于二次项系数为1的一元二次方程,他的两根之和等于一次项系数的相反数,两根之积等于常数项。
③推论2可以看作推论1的逆定理,利用推论2可以直接求出以两个数x1、x2为根的一元二次方程(二次项系数是1)是x2-(x1+x2)x+x1x2=0
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![关于的方程x2+(m+3)x-2+m=0的两实根互为相反数,则m的值为[]A.±3B.3C.-3D.不存在-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/108/2019-05-01/741c77c89a1efa891915be58ee28f279.gif)