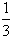6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张卡片洗匀后,正面向下放在桌上,另外还有与卡片上图形形状完全相同的地板砖若干块,所有地板砖的长都相等。(-九年级数学
题文
| 6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张卡片洗匀后,正面向下放在桌上,另外还有与卡片上图形形状完全相同的地板砖若干块,所有地板砖的长都相等。 (1)从这6张卡片中随机抽取一张,与卡片上图形形状相对应的这种地板砖能进行平面镶嵌的概率是多少? (2)从这6张卡片中随机抽取2张,利用列表或画树状图计算:与卡片上图形形状相对应的这两种地板砖能进行平面镶嵌的概率是多少? |
|
|
答案
解:(1) ; ;(2)根据题意得:  由上表可知,共有30种可能的结果,且每种结果的可能性相同,其中能进行平面镶嵌的结果有8种,分别是:AB, AD, BE, CF, BA, DA, EB, FC,  。 。 |
据专家权威分析,试题“6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张..”主要考查你对 利用概率解决问题,列举法求概率,平面图形的平铺和镶嵌 等考点的理解。关于这些考点的“档案”如下:
利用概率解决问题列举法求概率平面图形的平铺和镶嵌
考点名称:利用概率解决问题
- 应用概率可以解决以下问题:
(1)彩票中奖率的问题;
(2)抽样检测中产品合格率的问题;
(3)天气预报降水的概率;
(4)抛硬币、掷骰字的问题;
(5)圆盘分几个区域,分别涂色,转到哪个颜色的区域的概率;
(6)有刚回及无放回的摸球问题。
概率的应用情况远不止于这些,还有很多类似情况,在解决这类问题时,要充分理解题意,找到切入点,就能轻松的解决问题。
考点名称:列举法求概率
- 可能条件下概率的意义:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=
 。
。
等可能条件下概率的特征:
(1)对于每一次试验中所有可能出现的结果都是有限的;
(2)每一个结果出现的可能性相等。 - 概率的计算方法:
(1)列举法(列表或画树状图),
(2)公式法;
列表法或树状图这两种举例法,都可以帮助我们不重不漏的列出所以可能的结果。
列表法
(1)定义:用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法。
(2)列表法的应用场合
当一次试验要设计两个因素, 并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
树状图法
(1)定义:通过列树状图列出某事件的所有可能的结果,求出其概率的方法叫做树状图法。
(2)运用树状图法求概率的条件
当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率。
考点名称:平面图形的平铺和镶嵌
- 平面镶嵌:
用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地拼接在一起,这就是平面镶嵌。
用相同的正多边形镶嵌:只用一种多边形时,可以进行镶嵌的是三角形、四边形或正六边形。
用不同的正多边形镶嵌:
(1)用正三角形和正六边形能够进行平面镶嵌;
(2)用正十二边形、正六边形,正方形能够进行平面镶嵌。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图是一个木制圆盘,图中两同心圆,其中大圆直径为20cm,小圆的直径为10cm,一只小鸟自由自在地在空中飞行,小鸟停在小圆内(阴影部分)的概率是()。-九年级数学
下一篇:如图,有三个同心圆,由里向外的半径依次是2cm,4cm,6cm将圆盘分为三部分,飞镖可以落在任何一部分内,那么飞镖落在阴影圆环内的概率是()。-九年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |


![如图,转动转盘,转盘停止转动时指针指向阴影部分的概率是[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/116/2019-05-19/571e82d5a6a0366b53423682fba5f64b.gif)
![一个均匀的立方体六个面上分别标有数1,2,3,4,5,6。下图是这个立方体表面的展开图。抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的的概率是[]A、B、C、D、-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/116/2019-05-19/afe03013805201dd7c0a3b8b6d39e531.gif)
![从编号为1到10的10张卡片中任取1张,所得编号是3的倍数的概率为[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/116/2019-05-20/1bb75c757d66c522ea7ffc15841e3462.gif)
![在一个暗箱里,装有3个红球、5个黄球和7个绿球,它们除颜色外都相同,搅拌均匀后,从中任意摸出一个球是红球的概率是[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/116/2019-05-19/f0e84e9d734a37a2633ed58d0df722b9.gif)