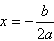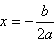题文

如图1，在直角坐标系中，已知点A（0，2）、点B（-2，0），过点B和线段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE。 （1 ）填空：点D 的坐标为（       ），点E 的坐标为（       ）。 （2 ）若抛物线经过A、D、E三点，求该抛物线的解析式。 （3）若正方形和抛物线均以每秒个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E落在y轴上时，正方形和抛物线均停止运动。 ①在运动过程中，设正方形落在y轴右侧部分的面积为s，求s关于平移时间t（秒）的函数关系式，并写出相应自变量t的取值范围。 ②运动停止时，求抛物线的顶点坐标。??

题型：解答题  难度：中档

答案

解：（1）D（-1，3）、E（-3，2）； （2）抛物线经过（0，2）、（-1，3）、（-3，2）， 则?? 解得  ? ∴； （3）①当点D运动到y轴上时，t=12，             当0＜t≤时，如下图? 设D'C'交y轴于点F? ∵?tan∠BCO==2，又∵∠BCO=∠FCC'? ∴?tan∠FCC'=2，即=2? ∵CC'=5t， ∴FC'=25t， ∴S△CC'F=CC'·FC'=t×t=5 t2； 当点B运动到点C时，t=1.? 当＜t≤1时，如下图 ? 设D'E'交y轴于点G，过G作GH⊥B'C'于H， 在Rt△BOC中，BC=? ∴GH=，∴CH=GH=? ∵CC'=t， ∴HC'=t-， ∴GD'=t-? ∴S梯形CC'D'G=； 当点E运动到y轴上时，t=，? 当1＜t≤时，如下图所示? 设D'E'、E'B'分别交y轴于点M、N? ∵CC'=t，B'C'=，∴CB'=t-， ∴B'N=2CB'=t- ∵B'E'=， ∴E'N=B'E'-B'N=-t? ∴E'M=E'N=(-t)? ∴S△MNE'=(-t)·(-t)=5t2  1/4    1 2 3 4 下一页 尾页 初中数学考试题 解答题  2 0） 过点B和线段OA的中点C作直线BC 以线段BC为边向上作正方形BCDE。（1）填空：点D的坐标为（） 点E的坐标为（）。（2）若抛物线经-九 最新内容 相关内容 网友推荐 图文推荐 二次函数y=ax2+bx+c的图像如图所示(2019-12-17) 已知实数a，b，c满足：a＜0，a-b+c(2019-05-20) 设a、b是常数，且b＞0，抛物线y=ax(2019-05-20) 已知二次函数y=ax2+bx+c（a≠0）的(2019-05-20) 若A（-4，y1），B（-3，y2），C（1(2019-05-20) 如图为抛物线y=ax2+bx+c的图象，A，(2019-05-20) 如图所示，二次函数y=ax2+bx+c（a≠(2019-05-20) 已知二次函数y=ax2+bx+c（a≠0）的(2019-05-20) 把抛物线y=-x2向上平移3个单位，则(2019-05-20) 大爱无痕 对每个孩子终身发展负责 书香中国·北京阅读季：构建“首善之区 阅读之部” 在学科和专业的交叉地带寻求“突围” 黄炎培职教思想研究会2019学术年会举办 2019中国纺织工业联合会科技教育奖励大会召开 《马克龙时代的法国教育观察》新书首发会举行 “阳光工程”诠释学校“清廉文化” 传承荣光与梦想 快乐体育“嗨”校园 二次函数y=ax2+bx+c的图像如图所示，则关于此二次函数 “劳动最美” 如图为二次函数y=ax2+bx+c的图象，(2019-05-20) 已知二次函数y=ax2+bx+c的图象如图(2019-05-20) 把抛物线y=2x2先向左平移4个单位，(2019-05-20) 若把函数y=x的图象用E（x，x）记，(2019-05-20) 下列四个图象表示的函数中，当x＜0(2019-05-20) 抛物线y=2x2+3x-4与y轴的交点坐标是(2019-05-20) 已知抛物线y=-x2+4x-3与x轴交于A、(2019-05-20) 抛物线y=x2向左平移1个单位，再向下(2019-05-20) 如图所示，四个函数图象对应的解析(2019-05-20) 若函数y=3x2与直线y=kx+3的交点为（(2019-05-20) 如图为二次函数y=ax2+bx+c的 已知二次函数y=ax2+bx+c的图 把抛物线y=2x2先向左平移4个 若把函数y=x的图象用E（x，x 下列四个图象表示的函数中， 上一篇：给出定义：设一条直线与一条抛物线只有一个公共点，只这条直线与这条抛物线的对称轴不平行，就称直线与抛物线相切，这条直线是抛物线的切线。有下列命题：①直线y=0是抛物线y=x-九年级数学     下一篇：抛物线y=（m﹣2）x2+2x+（m2﹣4）的图象经过原点，则m=()-九年级数学 零零教育社区：论坛热帖子 [家长教育] 孩子为什么会和父母感情疏离？ (2019-07-14) [教师分享] 给远方姐姐的一封信 (2018-11-07) [教师分享] 伸缩门 (2018-11-07) [教师分享] 回家乡 (2018-11-07) [教师分享] 是风味也是人间 (2018-11-07) [教师分享] 一句格言的启示 (2018-11-07) [教师分享] 无规矩不成方圆 (2018-11-07) [教师分享] 第十届全国教育名家论坛有感（二） (2018-11-07) [教师分享] 贪玩的小狗 (2018-11-07) [教师分享] 未命名文章 (2018-11-07) 栏目导航 有理数定义及分类 正数与负数 数轴 相反数 绝对值 比较有理数的大小 倒数 有理数加法 有理数减法 有理数的加减混合运算 有理数乘法 有理数除法 有理数的乘除混合运算 有理数的乘方 有理数的混合运算 近似数和有效数字 科学记数法和有效数字 实数的比较大小 无理数的定义 估算无理数的大小 实数的定义 数学常识 计算器的使用 写代数式 代数式的求值 去括号与添括号 整式的加减 单项式 多项式 同类项 探索规律 代数式的概念 整式的定义 一元一次方程的定义 一元一次方程的解法 一元一次方程中的待定系数 一元一次方程的应用 等式的性质 方程的定义 方程的解 等式的定义 二元一次方程的定义 二元一次方程组的定义 二元一次方程组的解法 二元一次方程组的应用 二元一次方程的应用 二元一次方程的解法 不等式的定义 不等式的性质 一元一次不等式的解法 一元一次不等式组的定义 一元一次不等式组的解法 一元一次不等式组的应用 不等式待定系数的取值范围 不等式的比较大小 一元一次不等式的应用 一元一次不等式的定义 函数的定义 变量及函数 常量与变量 函数值 函数的图像 正比例函数的定义 正比例函数的图像 一次函数的定义 一次函数的图像 求一次函数的解析式及一次函数的应用 一次函数与一元一次不等式（一元一次方程） 合并同类项 零指数幂（负指数幂和指数为1） 整式的乘法 整式的除法 公因式 因式分解 平方差公式 完全平方公式 整式的加减乘除混合运算 分式的定义 最简公分母 最简分式 分式的基本性质 分式的乘除 分式的加减 分式方程的定义 解分式方程 分式方程的应用 分式的加减乘除混合运算及分式的化简 反比例函数的定义 反比例函数的图像 反比例函数的性质 求反比例函数的解析式及反比例函数的应用 平均数 中位数和众数 极差 方差 二次根式的定义 二次根式的乘除 二次根式的加减 平方根 立方根 算术平方根 同类二次根式 二次根式的加减乘除混合运算，二次根式的化简 最简二次根式 实数的运算 一元二次方程的定义 一元二次方程的解法 一元二次方程根与系数的关系 一元二次方程的应用 一元二次方程根的判别式 随机事件 必然事件 概率的意义 列举法求概率 利用频率估算概率 利用概率解决问题 二次函数的定义 二次函数的图像 二次函数的最大值和最小值 求二次函数的解析式及二次函数的应用 二次函数与一元二次方程 二次函数与不等式（组） 全面调查和抽样调查 频数与频率 直方图 条形图 扇形图 折线图 统计表 象形统计图 总体、个体、样本、样本容量 用样本估算总体 二元多次（二次以上）方程（组） 逻辑推理 三元（及三元以上）一次方程（组）的解法 三元（及三元以上）一次方程（组）的应用 直线，线段，射线 角的概念 角平分线的定义 余角，补角 看图形找规律 认识立体几何图形 认识平面图形 几何体的展开图 几何体的表面积，体积 点、线、面、体 截一个几何体 七巧板 对顶角，同位角，内错角，同旁内角 平行线的判定 平行线的性质，平行线的公理 平行线之间的距离 垂直的判定与性质 相交线 三角形的内角和定理 三角形的外角性质 三角形的稳定性 三角形的中线，角平分线，高线，垂直平分线 三角形的内心、外心、中心、重心 直角三角形的性质及判定 等腰三角形的性质，等腰三角形的判定 等边三角形 三角形的周长和面积 三角形的三边关系 三角形中位线定理 全等三角形的性质 三角形全等的判定 全等图形 用坐标表示轴对称 轴对称 勾股定理的逆定理 勾股定理 平行四边形的性质 平行四边形的判定 矩形，矩形的性质，矩形的判定 菱形，菱形的性质，菱形的判定 梯形，梯形的中位线 重心 正方形，正方形的性质，正方形的判定 中心对称 关于原点对称的点的坐标 图形旋转 垂直于直径的弦 圆心角，圆周角，弧和弦 点与圆的位置关系 直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离） 圆和圆的位置关系（圆和圆的相离，圆与圆的相交，圆与圆的相切） 正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算） 弧长的计算 扇形面积的计算 圆锥的计算 圆柱的计算 圆的认识 确定圆的条件 相似多边形的性质 相似三角形的判定 相似三角形的性质 相似三角形的应用 位似 黄金分割数 相似图形 比例的性质 平行线分线段成比例 解直角三角形 锐角三角函数的定义 特殊角三角函数值 同角三角函数的关系 互余两角三角函数的关系 投影 视图（盲区） 尺规作图 有序数对 用坐标表示位置 用坐标表示平移 平面直角坐标系 平面向量 多边形的内角和和外角和 平面图形的平铺和镶嵌 组合图形面积 多边形 命题，定理 平移 角平分线的性质 垂直平分线的性质 最新信息 二次函数y=ax2+bx+c的图像如图所示 已知实数a，b，c满足：a＜0，a-b+c 设a、b是常数，且b＞0，抛物线y=ax 已知二次函数y=ax2+bx+c（a≠0）的 若A（-4，y1），B（-3，y2），C（1 如图为抛物线y=ax2+bx+c的图象，A， 如图所示，二次函数y=ax2+bx+c（a≠ 已知二次函数y=ax2+bx+c（a≠0）的 把抛物线y=-x2向上平移3个单位，则 小明同学观察如图所示的二次函数y= 热门信息 如图为二次函数y=ax2+bx+c的图象， 已知二次函数y=ax2+bx+c的图象如图 把抛物线y=2x2先向左平移4个单位， 若把函数y=x的图象用E（x，x）记， 下列四个图象表示的函数中，当x＜0 抛物线y=2x2+3x-4与y轴的交点坐标是 已知抛物线y=-x2+4x-3与x轴交于A、 抛物线y=x2向左平移1个单位，再向下 如图所示，四个函数图象对应的解析 若函数y=3x2与直线y=kx+3的交点为（ Copyright 2021 零零教育信息网 @ Powered By 零零教育信息网 ，这是一个公共的免费分享平台 网站导航联系我们广告合作豫ICP备09039788号 个人中心 服务邮箱 服务邮箱 7720015@qq.com 微信咨询 返回顶部 网站首页 联系我 微信咨询 个人中心 X 截屏，微信识别二维码 微信号：ten00_cn （点击微信号复制，添加好友）   打开微信 微信号已复制，请打开微信添加咨询详情！ 新闻 图书