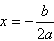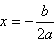证明:无论a取任何实数值时,抛物线y=x2+(a+1)x+12a+14是通过一个定点,而且这些抛物线的顶点都在一条确定的抛物线上.-数学
题文
证明:无论a取任何实数值时,抛物线y=x2+(a+1)x+
|
答案
证明:y=x2+(a+1)x+
当x=-
即无论a取任何实数时,已知抛物线总通过点M(-
又y=x2+(a+1)x+
故抛物线的顶点坐标为(-
即
y=-(x+
这条曲线是一条抛物线,即原抛物线的顶点都在一条确定的抛物线上. |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |