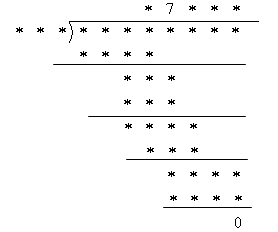
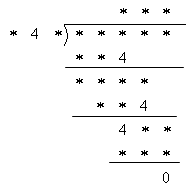
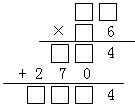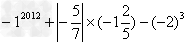已知b≥0,且a+b=c+1,b+c=d+2,c+d=a+3,求a+b+c+d的最大值.-数学
题文
| 已知b≥0,且a+b=c+1,b+c=d+2,c+d=a+3,求a+b+c+d的最大值. |
答案
| ∵a+b=c+1,b+c=d+2,c+d=a+3, ∴2b+c=6,c=6-2b, 代入a+b=c+1得a=7-3b, 代入b+c=d+2得d=4-b, 则a+b+c+d=17-5b, 因为b≥0, 所以当b取0时,a+b+c+d的最大值为17. |
据专家权威分析,试题“已知b≥0,且a+b=c+1,b+c=d+2,c+d=a+3,求a+b+c+d的最大值.-数学..”主要考查你对 有理数的乘除混合运算 等考点的理解。关于这些考点的“档案”如下:
有理数的乘除混合运算
考点名称:有理数的乘除混合运算
- 有理数的乘除混合运算:
可统一化为乘法运算,在进行乘除运算时,一般地,遇除化乘,转化为有理数的乘法进行计算。 - 乘除混合运算需要掌握:
1.由负因数的个数确定符号;
2.小数化成分数,带分数化成假分数;
3.除号改成称号,除号改成倒数,变成连乘形式;
4.进行约分;
5.注意运算顺序,乘除为同级运算,要遵守从左到右的顺序计算;
6.转化为乘法后,可运用乘法运算律简化运算。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |