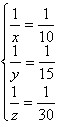某商场准备购进两种型号的摩托车共25辆,预计投资10万元.现有甲、乙、丙三种摩托车,甲种每辆4200元,可获利400元;乙种每辆3700元,可获利350元;丙种每辆3200元,可获利32-数学
题文
| 某商场准备购进两种型号的摩托车共25辆,预计投资10万元.现有甲、乙、丙三种摩托车,甲种每辆4200元,可获利400元;乙种每辆3700元,可获利350元;丙种每辆3200元,可获利320元.10万元资本全部用完. (1)请你帮助该商场设计进货方案; (2)从销售利润上考虑,应选择哪种方案? |
答案
(1)设购进甲种x辆,乙种y辆,则
解得:
设购进甲种m辆,丙种n辆,则
解得
设购进乙种a辆,丙种b辆,则
解得:
故进货方案由两种:①甲种进15辆,乙种进10辆;②甲种进20辆,乙种进5辆. (2)由(1)得,方案1的销售利润为: 400×15+350×10=9500元; 方案1的销售利润为: 400×20+320×5=9600. ∵9600>9500. ∴从销售利润上看要选择方案2. |
据专家权威分析,试题“某商场准备购进两种型号的摩托车共25辆,预计投资10万元.现有甲、..”主要考查你对 三元(及三元以上)一次方程(组)的应用 等考点的理解。关于这些考点的“档案”如下:
三元(及三元以上)一次方程(组)的应用
考点名称:三元(及三元以上)一次方程(组)的应用
- 三元一次方程组的应用:求待定系数的值,列方程组解应用题等。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需要花60元;经过协商,每种钢笔单价下降1元,结果只花了48元,-数学
下一篇:有三种物品,每件的价格分别是2元、4元和6元,现在用60元买这三种物品(三种物品均需买到),总数共买16件,而钱要恰好用完,则价格为6元的物品最多买几件?价格为2元的物品最少-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |