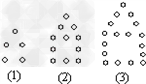
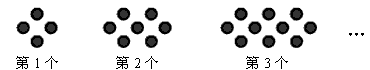古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,-七年级数学
题文
| 古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如: 他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…,这样的数为正方形数.下列数中既是三角形数又是正方形数的是 |
 |
| [ ] |
| A.15 B.25 C.55 D.1225 |
答案
| D |
据专家权威分析,试题“古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:他们研究..”主要考查你对 看图形找规律 等考点的理解。关于这些考点的“档案”如下:
看图形找规律
考点名称:看图形找规律
- 看图形找规律的题目也是比较常见的题目,作这种数学规律的题目,都会涉及到一个或者几个变化的量。所谓找规律,多数情况下,是指变量的变化规律。所以,抓住了变量,就等于抓住了解决问题的关键。
看图形找规律题步骤:
①寻找数量关系;
②用代数式表示规律;
③验证规律。
解题方法:
一、基本方法——看增幅
(一)如增幅相等(此实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n个数可以表示为:a+(n-1)b,其中a为数列的第一位数,b为增幅,(n-1)b为第一位数到第n位的总增幅。然后再简化代数式a+(n-1)b。
例:4、10、16、22、28……,求第n位数。
分析:第二位数起,每位数都比前一位数增加6,增幅相都是6,所以,第n位数是:4+(n-1)×6=6n-2
(二)如增幅不相等,但是,增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列)。如增幅分别为3、5、7、9,说明增幅以同等幅度增加。此种数列第n位的数也有一种通用求法。
基本思路是:
1、求出数列的第n-1位到第n位的增幅;
2、求出第1位到第第n位的总增幅;
3、数列的第1位数加上总增幅即是第n位数。
举例说明:2、5、10、17……,求第n位数。
分析:数列的增幅分别为:3、5、7,增幅以同等幅度增加。那么,数列的第n-1位到第n位的增幅是:3+2×(n-2)=2n-1,总增幅为:
〔3+(2n-1)〕×(n-1)÷2=(n+1)×(n-1)=n2-1
所以,第n位数是:2+ n2-1= n2+1
此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察凑的方法求出,方法就简单的多了。
(三)增幅不相等,但是,增幅同比增加,即增幅为等比数列,如:2、3、5、9,17增幅为1、2、4、8.
(四)增幅不相等,且增幅也不以同等幅度增加(即增幅的增幅也不相等)。此类题大概没有通用解法,只用分析观察的方法,但是,此类题包括第二类的题,如用分析观察法,也有一些技巧。二、基本技巧
(一)标出序列号:找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。找出的规律,通常包序列号。所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘。
例如,观察下列各式数:0,3,8,15,24,……。试按此规律写出的第100个数是什么。
解答这一题,可以先找一般规律,然后使用这个规律,计算出第100个数。我们把有关的量放在一起加以比较:
给出的数:0,3,8,15,24,……。
序列号: 1,2,3, 4, 5,……。
容易发现,已知数的每一项,都等于它的序列号的平方减1。因此,第n项是n2-1,第100项是1002-1。
(二)公因式法:每位数分成最小公因式相乘,然后再找规律,看是不是与n2、n3,或2n、3n,或2n、3n有关。
例如:1,9,25,49,( ),( ),的第n为(2n-1)2
(三)看例题:
A: 2、9、28、65.....增幅是7、19、37....,增幅的增幅是12、18 答案与3有关且............即:n3+1
B:2、4、8、16.......增幅是2、4、8.. .....答案与2的乘方有关即:2n
(四)有的可对每位数同时减去第一位数,成为第二位开始的新数列,然后用(一)、(二)、(三)技巧找出每位数与位置的关系。再在找出的规律上加上第一位数,恢复到原来。
例:2、5、10、17、26……,同时减去2后得到新数列: 0、3、8、15、24……,
序列号:1、2、3、4、5
分析观察可得,新数列的第n项为:n2-1,所以题中数列的第n项为:(n2-1)+2=n2+1
(五)有的可对每位数同时加上,或乘以,或除以第一位数,成为新数列,然后,在再找出规律,并恢复到原来。
例 : 4,16,36,64,?,144,196,… ?(第一百个数)
同除以4后可得新数列:1、4、9、16…,很显然是位置数的平方。
(六)同技巧(四)、(五)一样,有的可对每位数同加、或减、或乘、或除同一数(一般为1、2、3)。当然,同时加、或减的可能性大一些,同时乘、或除的不太常见。
(七)观察一下,能否把一个数列的奇数位置与偶数位置分开成为两个数列,再分别找规律。三、基本步骤
1、先看增幅是否相等,如相等,用基本方法(一)解题。
2、如不相等,综合运用技巧(一)、(二)、(三)找规律
3、如不行,就运用技巧(四)、(五)、(六),变换成新数列,然后运用技巧(一)、(二)、(三)找出新数列的规律
4、最后,如增幅以同等幅度增加,则用用基本方法(二)解题。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |