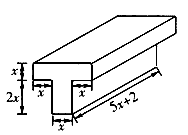
如果对一个长方体观察所得的左视图、主视图、俯视图的面积都相同,那么这个长方体是正方体吗?-七年级数学
题文
| 如果对一个长方体观察所得的左视图、主视图、俯视图的面积都相同,那么这个长方体是正方体吗? |
答案
| 解:设长方体的长,宽,高分别为a,b,c. ∴左视图的面积为bc,主视图的面积为ac,俯视图的面积为ab, ∴bc=ac=ab, ∴a=b=c, ∴这个长方体是正方体. |
据专家权威分析,试题“如果对一个长方体观察所得的左视图、主视图、俯视图的面积都相同..”主要考查你对 几何体的表面积,体积,视图(盲区) 等考点的理解。关于这些考点的“档案”如下:
几何体的表面积,体积视图(盲区)
考点名称:几何体的表面积,体积
- 几何体的表面积和体积要求:
认识柱、锥、台、球及其简单组合体的结构特征,了解柱、锥、台、球的概念;
了解柱、锥、台、球的表面积与体积的计算,并能运用公式计算柱、锥、台、球及其简单组合体的表面积与体积。 - 几何体一般概念及性质:
1、圆柱:可以看做以矩形的一边为旋转轴、旋转一周形成的曲面所围成的几何体
2、圆锥:可以看做以直角三角形的一直角边为旋转轴、旋转一周形成的曲面所围成的几何体
3、圆台:可以看做以直角梯形中垂直于底边的腰所在的直线为旋转轴、旋转一周形成的曲面所围成的几何体
4、球:一个半圆绕着它的直径所在的直线旋转一周所形成的曲面所围成的几何体
5、棱柱有两个面互相平行、而其余每相邻两个面的交线都互相平行
6、多面体是由若干个平面多边形所围成的几何体
7、棱锥有一个面是多边形,而其余个面都是有一个公共顶点的三角形 几何体的表面积,体积计算公式:
1、圆柱体:
表面积:2πRr+2πRh
体积:πR2h (R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:
表面积:πR2+πR[(h2+R2)的平方根]
体积: πR2h/3 (r为圆锥体低圆半径,h为其高,3、正方体:
a-边长,
S=6a2 ,V=a34、长方体:
a-长 ,b-宽 ,c-高
S=2(ab+ac+bc) V=abc5、棱柱:
S-底面积 h-高
V=Sh6、棱锥 :
S-底面积 h-高
V=Sh/37、棱台:
S1和S2-上、下底面积 h-高
V=h[S1+S2+(S1S2)^1/2]/38、拟柱体:
S1-上底面积 ,S2-下底面积 ,S0-中截面积 h-高,
V=h(S1+S2+4S0)/69、圆柱:
r-底半径 ,h-高 ,C—底面周长 S底—底面积 ,S侧—侧面积 ,S表—表面积
C=2πr S底=πr2,S侧=Ch ,S表=Ch+2S底 ,V=S底h=πr2h10、空心圆柱:
R-外圆半径 ,r-内圆半径 h-高
V=πh(R^2-r^2)11、直圆锥 :
r-底半径 h-高
V=πr^2h/312、圆台:
r-上底半径 ,R-下底半径 ,h-高
V=πh(R2+Rr+r2)/313、球:
r-半径 d-直径
V=4/3πr^3=πd^3/614、球缺
h-球缺高,r-球半径,a-球缺底半径
V=πh(3a2+h2)/6 =πh2(3r-h)/315、球台:
r1和r2-球台上、下底半径 h-高
V=πh[3(r12+r22)+h2]/616、圆环体:
R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径
V=2π2Rr2 =π2Dd2/417、桶状体:
D-桶腹直径 d-桶底直径 h-桶高
V=πh(2D2+d2)/12 ,(母线是圆弧形,圆心是桶的中心)
V=πh(2D2+Dd+3d2/4)/15 (母线是抛物线形)
考点名称:视图(盲区)
- 视图定义:
当我们从某一角度观察一个实物时,所看到的图像叫做物体的一个视图。
物体的三视图特指主视图、俯视图、左视图。
主视图:在正面内得到的由前向后观察物体的视图,叫做主视图。
俯视图:在水平面内得到的由上向下观察物体的视图,叫做俯视图。
左视图:在侧面内得到的由左向右观察物体的视图,叫做左视图,有时也叫做侧视图。
人在观察目标时,从眼睛到目标的射线叫做视线,眼睛所在的位置叫做视点,有公共视点的两条视线所称的角叫做视角。
我们把视线不能到达的区域叫做盲区。 - 盲区特征:
①人离障碍物越近,盲区越大;
②将视点与障碍物的顶点连线,交地面于一点,此点即是盲区与非盲区的分界点。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |


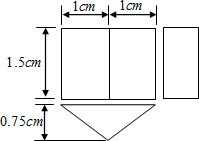
![棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积为[]A.36cm2B.33cm2C.30cm2D.27cm2-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/145/2020-01-04/542bcb9e7315c5bf2425db8e467ae6bc.png)