一个几何体的三视图如下图所示,则这个几何体的名称是______.并根据三视图画出它的平面展开图,并求其表面积S.-数学
题文
一个几何体的三视图如下图所示,则这个几何体的名称是______.并根据三视图画出它的平面展开图,并求其表面积S.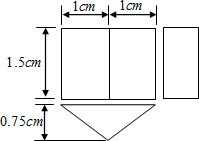 |
题文
一个几何体的三视图如下图所示,则这个几何体的名称是______.并根据三视图画出它的平面展开图,并求其表面积S. |
答案
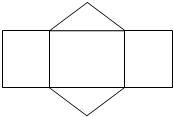 这个几何体的名称是三棱柱; 平面展开图如图所示; 由三视图可知,三棱柱的底面是等腰三角形,腰长为
∴S表面积=2S底面积+S侧面积=2×
故答案为三棱柱. |
据专家权威分析,试题“一个几何体的三视图如下图所示,则这个几何体的名称是______.并根..”主要考查你对 几何体的表面积,体积,勾股定理,视图(盲区) 等考点的理解。关于这些考点的“档案”如下:
几何体的表面积,体积勾股定理视图(盲区)
考点名称:几何体的表面积,体积
几何体的表面积,体积计算公式:
1、圆柱体:
表面积:2πRr+2πRh
体积:πR2h (R为圆柱体上下底圆半径,h为圆柱体高)
2、圆锥体:
表面积:πR2+πR[(h2+R2)的平方根]
体积: πR2h/3 (r为圆锥体低圆半径,h为其高,
3、正方体:
a-边长,
S=6a2 ,V=a3
4、长方体:
a-长 ,b-宽 ,c-高
S=2(ab+ac+bc) V=abc
5、棱柱:
S-底面积 h-高
V=Sh
6、棱锥 :
S-底面积 h-高
V=Sh/3
7、棱台:
S1和S2-上、下底面积 h-高
V=h[S1+S2+(S1S2)^1/2]/3
8、拟柱体:
S1-上底面积 ,S2-下底面积 ,S0-中截面积 h-高,
V=h(S1+S2+4S0)/6
9、圆柱:
r-底半径 ,h-高 ,C—底面周长 S底—底面积 ,S侧—侧面积 ,S表—表面积
C=2πr S底=πr2,S侧=Ch ,S表=Ch+2S底 ,V=S底h=πr2h
10、空心圆柱:
R-外圆半径 ,r-内圆半径 h-高
V=πh(R^2-r^2)
11、直圆锥 :
r-底半径 h-高
V=πr^2h/3
12、圆台:
r-上底半径 ,R-下底半径 ,h-高
V=πh(R2+Rr+r2)/3
13、球:
r-半径 d-直径
V=4/3πr^3=πd^3/6
14、球缺
h-球缺高,r-球半径,a-球缺底半径
V=πh(3a2+h2)/6 =πh2(3r-h)/3
15、球台:
r1和r2-球台上、下底半径 h-高
V=πh[3(r12+r22)+h2]/6
16、圆环体:
R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径
V=2π2Rr2 =π2Dd2/4
17、桶状体:
D-桶腹直径 d-桶底直径 h-桶高
V=πh(2D2+d2)/12 ,(母线是圆弧形,圆心是桶的中心)
V=πh(2D2+Dd+3d2/4)/15 (母线是抛物线形)
考点名称:勾股定理
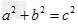 。
。| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |