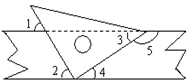
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F。试判断BE与DF的位置关系,并说明你的理由。-七年级数学
题文
如图,四边形ABCD中,∠A =∠C = 90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F。试判断BE与DF的位置关系,并说明你的理由。 |
答案
| 平行(可证明∠AFD=∠ABE) |
试题分析:依题意知,四边形ADBC中,∠A =∠C = 90°,则∠B +∠ADC= 360°-∠A -∠C=180°。因为BE平分∠ABC交CD于E,DF平分∠ADC交AB于F,则可知∠ABE+∠ADF=90°。且∠AFD+∠ADF=90°。 所以∠AFD=∠ABE。所以BE∥DF。 点评:本题难度中等,主要考查学生对平行线性质和判定的学习掌握。运用多边形内角和求对角互补为解题关键。 |
据专家权威分析,试题“如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC..”主要考查你对 点、线、面、体 等考点的理解。关于这些考点的“档案”如下:
点、线、面、体
考点名称:点、线、面、体
- 点动成线,线动成面,面动成体:
长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体。
包围着体的是面,面有平的面和曲的面两种。
夜晚流星划过天空时留下一道明亮的光线,节日的焰火画出的曲线组成优美的图案,这些都给我们以线的形象,面和面相交的地方形成线。
天上的星星、世界地图上的城市等都给我们以点的形象,线和线相交的地方是点。
几何图形都是由点、线、面、体组成的,点是构成图形的基本元素。 - 常见几何体的三视图:


- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图,已知∠1=∠C,∠2=∠3,BE是否平分∠ABC?请说明理由。-七年级数学
下一篇:如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AD∥BC,AEBD.请完成下列证明过程.证明:∵∠5=∠6∴AB∥()∴∠3=()∵∠3=∠4∴∠4=∠BDC()∴∥BD()∴∠2=∵∠1=∠2∴∠1=∴AD∥BC()-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |